PBRT 形体 续
3.6 三角形和网格
class TriangleMesh : public Shape {
public:
protected:
};
三角形是计算机图形学中最常用的形体。pbrt支持三角形网格,它可以存放很多的三角形,这些三角形可以共享顶点数据(per-vertex data)。而单个的三角形可以简单地被视为退化的网格。
TriangleMesh构造器的变量为:
· nt: 三角形个数。
· nv: 顶点个数。
· vi : 指向一个顶点索引值数组的指针。对于第i个三角形,其三个顶点位置是P[vi[3*i]], P[vi[3*i+1]]和P[vi[3*i+2]]。
· P: 存储nv个顶点位置的数组。
· N: 一个可选的法向量数组,网格中每个顶点都对应其中的一个法向量。如果该数组存在的话,通过对它们进行插值,来计算三角形内的点的着色微分几何信息。
· S:一个可选的切向量数组,网格中每个顶点都对应其中的一个切向量。这些切向量也用来计算着色几何信息。
· uv: 一个可选的(u,v)参数数组, 每个顶点都对应一个(u,v)。
构造器把相关的信息拷贝并存放在TriangleMesh对象中。要注意的是,它必须保留vi, P, N和S的拷贝,因为调用者拥有对所传入的数据的所有权。
在pbrt中,三角形扮演着双重角色:既可作为用户所提供的基本几何体,又可以是其它基本几何体细分成三角形网格的结果。例如,细分曲面(subdivision surface)要创建一个三角形网格来逼近平滑的极限曲面(limit surface)。光线求交是对这些三角形进行的,而不是直接跟细分曲面进行的。
由于三角形的第二个角色,创建三角形网格的例程应该说明三角形的参数化方式。例如,如果通过计算参数曲面上的三个(u,v)坐标的位置而创建出一个三角形,那么,想求得三角形内的交点的(u,v)值,就要通过对这些(u,v)值插值而得到。
TriangleMesh:: TriangleMesh(const Transform &o2w, bool ro, int nt, int nv,
const int *vi, const Point *P, const Normal *N, const Vector *S, float *uv)
: Shape(o2w, ro) {
ntris = nt;
nverts = nv;
vertexIndex = new int[3 * ntris];
memcpy(vertexIndex, vi, 3 * ntris * sizeof(int));
}
片段
int ntris, nverts;
int vertexIndex;
Point *p;
Normal *n;
Vector *s;
float *uvs;
前面所介绍过的二次曲面都是在物体空间中定义,并把光线从世界空间变换到物体空间;而三角形网格则不同:它把形体变换到世界空间,省去了把光线变换到物体空间的工作,也省去了把交点的微分几何信息变换到世界空间的工作。这是一个很不错的方法,因为,这个变换工作是在系统开始时进行的,从而在渲染过程中避免了很多次的光线变换。实际上,对于二次曲面也可以这样做,但很复杂。用于着色运算的法向量和切向量在物体空间中保持不变,因为GetShadingGeometry()必须使用所传入的变换矩阵进行物体到世界空间的变换,而不一定用存储在Shape中的变换矩阵。
for (int i = 0; i < nverts; ++i)
p = ObjectToWorld(P);
三角形网格在物体空间中的包围盒很容易计算,因为它就是包含所有顶点的包围盒。但是,所有顶点在构造器中已经被变换到了世界空间,我们还需把它们变换回物体空间中,才能求物体空间中的包围盒。注意这个计算还是很费时的,如果这些包围盒可以被再利用,就应该暂存(cache)这些包围盒。
BBox TriangleMesh::ObjectBound() const {
BBox bobj;
for (int i = 0; i < nverts; i++)
bobj = Union(bobj, WorldToObject(p));
return bobj;
}
世界空间中的包围盒是很容易求得的:
BBox TriangleMesh::WorldBound() const {
BBox wolrdBounds;
for (int i = 0; i < nverts; i++)
wolrdBounds = Union(wolrdBounds, p);
return wolrdBounds;
}
TriangleMesh形体不可以直接用来计算交点。实际上,它把自己分解成许多单个的Triangle对象,每一个对象代表一个三角形。所有这些单独的三角形引用数组p的顶点,这样就避免了对共享数据的复制。因此,TriangleMesh要重写Shape::CanIntersect(),来表示它不能直接求交。
Bool CanIntersect() const { return false; }
当pbrt遇到一个不能直接求交的形体时,会调用形体的Refine()。Shape::Refine()要生成一个包含更简单形体的列表。这里的实现很简单,它只是为网格中的每个三角形创建一个Triangle对象,并放在列表中。
void TriangleMesh::Refine(vector
for(int i = 0; i < ntris; i++)
refined.push_back(new Triangle(ObjectToWorld,
reverseOrientation, (TriangleMesh *)this, i));
}
3.6.1 三角形
class Triangle : public Shape {
public :
private:
};
Triangle类并不存储太多数据,它只有一个指向其父对象TriangleMesh的指针和一个指向其三个顶点索引值的指针。
Triangle(const Transform &o2w, bool ro, TriangleMesh *m, int n)
:Shape(o2w, ro) {
mesh = m;
v = &mesh->vertexIndex[3*n];
}
注意到该实现只存放指向第一个顶点索引值的指针,而不是存放三个指向其三个顶点的指针。我们以多了一层间接引用为代价,节省了每个Triangle的存储空间。
Reference
int *v;
跟TriangleMesh类似,我们有下面求包围盒的方法:
BBox Triangle::ObjectBound() const {
return Union(BBox(WorldToObject(p1), WorldToObject(p2),
WorldToObject(p3));
}
BBox Triangle::WorldBound() const {
return Union(BBox( p1,p2), p3);
}
const Point &p1 = mesh->p[v[0]];
const Point &p2 = mesh->p[v[1]];
const Point &p3 = mesh->p[v[2]];
3.6.2 三角形求交
利用重心坐标系(barycentric coordinates)我们可以推导出非常高效的光线和三角形的求交算法。
【补充一个定理: 对于三角形P0P1P2内的任何一点P,都存在唯一的三个非负实数b1,b2,b3 使得P= b1P1 +b2P2+b3P3, 且b1+b2+b3=1。 这是重心坐标系的基础。】
重心坐标系提供了一个用两个变量b1和b2参数化三角形的方法:
p(b1,b2) = (1 – b1 – b2)p0 + b1p1 +b2p2, 且b1>=0, b2>=0, b1+b2 <=1 很自然地,我们可以利用重心坐标对三角形内的点进行插值。给定三个顶点上的值a0,a1和a2和三角形内一点的重心坐标,我们可以通过插值求得在该点的a值,即:(1-b1-b2)a0+b1a1+b2a2。 为了推导光线跟三角形的求交算法,我们把光线方程代入三角形方程: o + td = (1-b1-b2)p0 + b1p1 + b2p2 利用Moller和Trumbore(1997)所描述的技术,我们用简记e1 = p1 – p0, e2 = p2 – p1, s = o – p0, 重写上面的方程,得到下面的矩阵方程:
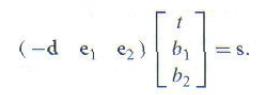
通过求解这个线性方程组,可以得到交点的重心坐标和其沿光线的参数距离。
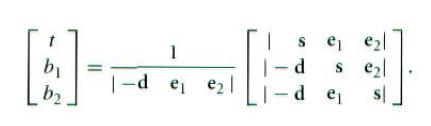
我们用克莱姆法则求解该方程组。为了简洁,我们记| a b c| 为以 a b c为列的行列式值。根据克莱姆法则,有:
利用等式| a b c| = – (a x c) . b = – (c x b) . a,我们得到:
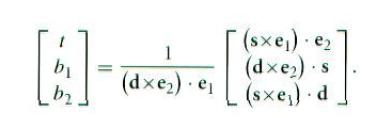
用 s1 = d x e2 和 s2 = s x e1进行替换, 结果就更清楚了:

计算e1,e2,s需要9个减法。计算s1,s2需要2个叉积,即12个乘法和6个减法。最后,计算t,b1,b2需要4个点积 (12个乘法和8个加法),一个求倒数,和三个乘法。这样,光线和三角形的求交总花费是1个除法,27个乘法,17个加(减)法。注意如果在算法的中间过程中发现没有交点,有些运算是可以省去的。
bool Triangle::Intersect(const Ray &ray, float *tHit, DifferentialGeometry *dg) const {
*tHit = t;
return true;
}
首先我们计算上面公式的分母。算法先找到三角形的三个顶点,然后得出边向量和这个分母。如果分母为零,则没有交点。
Vector e1 = p2 – p1;
Vector e2 = p3 – p1;
Vector s1 = Cross(ray.d, e2);
float divisor = Dot(s1, e1);
if(divisor == 0.)
return false;
float invDivisor = 1.f / divisor;
现在我们可以计算重心坐标b1。回忆一下:如果重心坐标小于0或大于1,则表示点在三角形之外,即没有交点。
Vector d = ray.o – p1;
float b1 = Dot(d, s1) * invDivisor;
if( b1 < 0. || b1 > 1.)
return false;
第二个重心坐标b2可以用相似的方法得到:
Vector s2 = Cross(d, e1);
float b2 = Dot(ray.d, s2) * invDivisor;
if( b2 < 0. || b1+ b2 > 1.)
return false;
我们得知有交点后,就可以计算交点沿光线的距离。如果求得的t值不在Ray::mint和Ray::maxt之间,则没有交点。
float t = Dot(e2, s2) * invDivisor;
if ( t < ray.mint || t > ray.maxt)
return false;
到此为止,我们有了初始化DifferentialGeometry结构的所有信息。跟前面介绍的形体不同,没有必要把偏导数变换到世界空间,因为三角形顶点已经被变换到世界空间了。跟圆盘一样,三角形上的法向量的偏导数为零,因为这是个平面。
为了生成一致的切向量,我们要用(u,v)参数值计算三角形顶点处的偏导数dp/du,dp/dv。虽然三角形上所有点的偏导数相同,但我们还是为每个交点重新计算一次偏导数。通过这些冗余的计算,可以节省大量的存储空间。
三角形是下列公式所表示的点的集合:

其中p0是某个点,u和v是三角形的参数坐标。我们也知道三个点位置pi,i = 1,2,3,以及每个顶点上的纹理坐标(ui,vi)。偏导数应该满足下列条件:

换句话说,存在一个唯一的仿射变换把从二维(u,v)空间的点变换到三角形上的点(即使三角形是三维的,该变换也存在,因为三角形是在一个平面上)。为了计算dp/du,dp/dv,我们计算p1-p2和p2-p3,得到下列矩阵方程:
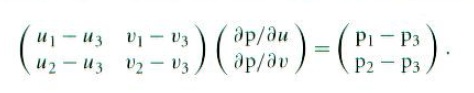
所以就有:
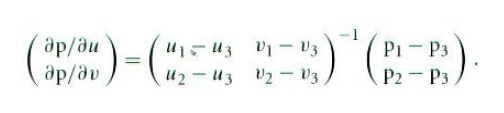
其中2×2矩阵的逆阵是:
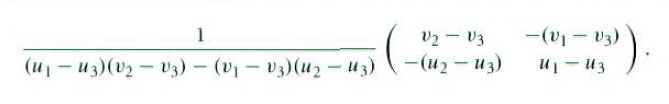
Vector dpdu, dpdv;
float uvs[3][2];
GetUVs(uvs);
float determinant = du1 * dv2 – dv1 * du2;
if(determinant == 0.f) {
}
else {
float invdet = 1.f / determinant;
dpdu = (dv2 * dp1 – dv1 * dp2) * invdet;
dpdv = -(du2 * dp1 + du1 * dp2) * invdet;
}
float du1 = uvs[0][0] – uvs[2][0];
float du2 = uvs[1][0] – uvs[2][0];
float dv1 = uvs[0][1] – uvs[2][1];
float dv2 = uvs[1][1] – uvs[2][1];
Vector dp1 = p1 – p3, dp2 = p2 – p3;
最后要处理矩阵是奇异矩阵的特殊情况,注意这只有当用户提供的顶点参数值是退化的时候才有可能发生。这时,Triangle类只选择一个由三角形法向量生成的任意坐标系,这样保证了它们是正交的。
CoordinateSystem(Normalize(Cross(e2, e1)), &dpdu, &dpdv);
为了计算交点处的(u,v)值,要利用三个顶点的(u,v)值和重心坐标公式:
float b0 = 1 – b1 – b2;
float tu = b0 * uvs[0][0] + b1 * uvs[1][0] + b2 * uvs[2][0];
float tv = b0 * uvs[0][1] + b1 * uvs[1][1] + b2 * uvs[2][1];
GetUVs()是个辅助函数,它返回三个三角形顶点的(u,v)坐标, 要么从TriangleMesh取得,要么取缺省值。
void Triangle::GetUVs(float uv[3][2]) const {
if(mesh->uvs) {
uv[0][0] = mesh->uvs[2*v[0]];
uv[0][1] = mesh->uvs[2*v[0] +1];
uv[1][0] = mesh->uvs[2*v[1]];
uv[1][1] = mesh->uvs[2*v[1]+1];
uv[2][0] = mesh->uvs[2*v[2]];
uv[2][1] = mesh->uvs[2*v[2]+1];
}
else {
uv[0][0] = 0.; uv[0][1] = 0.;
uv[1][0] = 1.; uv[0][1] = 0.;
uv[2][0] = 1.; uv[0][1] = 1.;
}
3.6.3 表面面积
回忆一下第2.2节,平行四边形的面积等于沿其两个相邻边的向量的叉积的长度。从这一点很容易看出,三角形的面积是该叉积长度的一半。
float Triangle::Area() const {
return 0.5f * Cross(p2 – p1, p3 – p1).Length();
}
3.6.4 着色几何信息
如果TriangleMesh有关于顶点的法向量或切向量,GetShadingGeometry()就利用它们初始化着色几何信息。
virtual void GetShadingGeometry(const Transform &obj2world, const DifferentialGeometry &dg,
DifferentialGeometry *dgShading) const {
If(!mesh->n && !mesh->s) {
*dgShading = dg;
return;
}
}
由于从光线求交例程得到的DifferentialGeometry存有参数(u,v),但并不存放交点的重心坐标系下的坐标,所以第一个任务是求其重心坐标系坐标。因为DifferentialGeometry的构造器需要两个切向量,我们还要计算插值的法向量和s向量,再将它们转换成两个切向量。最后,我们求得着色用的法向量的偏导数,就可以初始化着色几何结构了。
回忆一下,三角形的DifferentialGeometry中的参数坐标(u,v)是通过对三角形顶点上的参数值插值而得到的:
u = b0u0 + b1u1 + b2u2
v = b0v0 + b1v1 + b2v2
其中 b0 = 1 – b1 – b2。这里,u,v,ui,vi都是已知的,u和v来自DifferentialGeometry, ui,vi来自Triangle。我们把上面两式中的b0用1-b1-b2替换掉,再整理得到关于b1和b2的线性方程组:
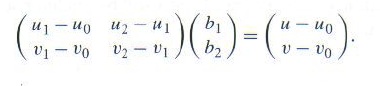
这是具有基本形式AB=C的线性方程组, 求出A的逆阵就得到B:
B = A-1C
求解这类线性方程组的封闭解(closed-form solution)的实现是辅助函数SolveLinearSystem2x2().
float b[3];
if(!SolveLinearSystem2x2(A, C, &b[1])) {
}
else
b[0] = 1.f – b[1] – b[2];
float uv[3][2];
GetUVs(uv);
float A[2][2] =
{ { uv[1][0] – uv[0][0], uv[2][0] – uv[0][0] },
{ uv[1][1] – uv[0][1], uv[2][1] – uv[0][1] }};
float C[2] = {dg.u – uv[0][0], dg.v – uv[0][1]};
如果A的行列式值为零,则没有解,SolveLinearSystem2x2()返回false。当三个三角形顶点都有相同的纹理坐标时会出现这种情况。这时我们把它们的重心坐标都设为1/3。
b[0] = b[1] = b[2] = 1.f/3.f;
得到重心坐标以后,通过对相应的顶点法向量和切向量进行插值,就可以计算出着色用的法向量和s切向量。首先,DifferentialGeometry所用的ts向量可以由ss和ns的叉积得到,这是所要求的两个正交向量中的一个。下一步,用ns和ts的叉积覆盖ss的值,再用ss和ts的叉积得到ns。
这样一来,如果提供了顶点上n和s向量,当n和s插值后所得到的向量并不正交时,n保持不变,s要做些修正,使得两者保持正交。
计算偏导数dn/du,dn/dv的方法跟计算dp/du,dp/dv的很相似,这里就不提了。
3.7 细分曲面
在本章的最后,我们定义实现细分曲面的形体,它可以很好地描述复杂的平滑形体。一个多边形网格所对应的细分曲面是通过重复地细分网格上的多边形而生成的,在这个细分过程中,新的多边形顶点位置是由旧的多边形顶点的加权组合而得到的。
选定好细分规则后,这个细分过程如果无限地进行下去,就会逼近一个平滑的极限曲面。实际上,通常通过很少几步的细分,其结果就跟极限曲面很相似了。
虽然细分曲面的研究始于七十年代,但跟曲面的多边形表示和样条表示比较而言,细分曲面有着非常重要的优势,所以在计算机图形学领域中,细分曲面得到了相当的重视。其优势表现在:
· 细分曲面是平滑的,而多边形网格则不同:无论模型做得多么精细,只要靠近仔细观察,就会看到许多平坦的刻面。
· 现有的许多造型系统的基本技术仍可以用到细分曲面上。那些面向多边形网格的造型技术可以用来构造细分曲面的控制网格。
· 细分曲面非常适合于描述有着复杂拓扑结构的形体,因为它们的控制网格可以有任意复杂的拓扑结构。而参数化的曲面模型则无法处理好复杂的拓扑结构。
· 细分曲面方法常常是样条曲面表示的一般化方法,细分曲面的渲染器可以渲染样条曲面。
· 很容易对一个细分曲面的局部添加细节,只要对相应的控制网格添加多边形就可以了。而这对样条曲面而言,就困难得多。
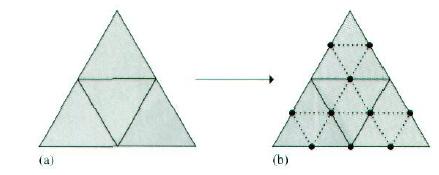
这里我们要描述的是Loop细分曲面的实现(Charles Loop在他的硕士论文中发明了该技术,故名Loop细分曲面)。Loop细分曲面的控制网格是由三角形构成的,多于三个顶点的多边形要化为多个三角形才可以使用。在每步细分过程中,所有面要划分成四个子面。新顶点是沿着原网格的边被添加进来的,它们的位置由附近顶点的加权平均值而得到。并且,原顶点的位置也要更新为其原位置和新添加的邻近顶点位置的加权平均值。这里所实现的技术是Hoppe et al(1994)对Loop方法的改进形式。我们不讨论这些权值是如何推导出来的。通过数学上的证明可以得知这些权值确实保证了极限曲面具有我们想要的平滑性。
3.7.1 网格的表示
class LoopSubdiv : public Shape {
public:
private:
};
我们开始描述表示细分曲面的数据结构。为了清晰地实现细分算法中的所有操作,这些数据结构需要精心的设计。传入LoopSubdiv构造器的参数声明了一个三角形网格,其格式跟TriangleMesh构造器所用的完全相同[第3.6节]:每个面由三个顶点索引值表示,这些索引值给出了三个顶点在顶点数组P中的偏置量。我们需要这些数据来确定那些面是邻接面,那些面跟那些点邻接,等等。
LoopSubdiv::LoopSubdiv(const Transform &o2w, bool ro,
int nfaces, int nvertices, const int *vertexIndices,
const Point *P, int nl)
: Shape(o2w, ro) {
nLevels = nl;
}
我们稍后会定义一下SDVertex, SDFace结构,它们分别存放细分曲面的顶点数据和面数据。构造器先为网格的每个顶点申请一个SDVertex实例,也为每个面申请一个SDFace实例。它们暂时还没有被初始化。
int i;
SDVertex *verts = new SDVertex[nvertices];
for( i = 0; i < nvertices; ++i) {
verts = SDVertex(P);
vertices.push_back(&verts);
}
SDFace *fs = new SDFace[nfaces];
for (i = 0; i < nfaces; i++)
faces .push_back(&fs);
LoopSubdiv的析构器不在这里介绍了,它只是释放所有面和顶点的内存空间。
int nLevels;
vector
vector
Loop细分规则同其他细分规则一样,假定控制网格是不存在非交叠边的–即一个边最多有两个面共享。控制网格既可以是打开的也可以是闭合的: 闭合的网格没有边界,所有面都通过它们的边跟其他面相邻。而打开的网格存在一些少于三个邻接面的面。这两种网格LoopSubdiv都支持。
在三角形网格的内部,大多数顶点和6个面相连,并且有6个邻接的顶点通过边跟其相邻。在打开的网格的边界上,大多数顶点跟3个面和4个顶点相邻。直接跟一个顶点相邻的顶点数目叫做该顶点的价(valence)。我们把价不等于6的内部顶点和价不等于4的边界上的顶点称为非正规顶点,把其它的顶点称为正规顶点。Loop细分曲面除了在非正规顶点的地方,都是处处平滑的。
每个SDVertex存放了顶点的位置,一个指示其为正规或非正规顶点的布尔变量,还有一个只是其是否为边界顶点的布尔变量。它还有一个指向其任意一个邻接面的指针,我们可以从这个指针出发,来找到其他的邻接面。最后,还有一个指针来存放下一级细分所产生的新顶点。
struct SDVertex {
Point P;
SDFace *startFace;
SDVertex *child;
bool regular, boundary;
};
SDVertex的构造器只做简单的初始化工作, 注意SDVertex::startFace的值被设为NULL。
SDVertex(Point pt = Point(0,0,0))
: P(pt), startFace(NULL), child(NULL), regular(false), boundary(false) { }
网格的大部分拓扑信息存放在SDFace结构中。因为所有的面是三角形,SDFace保存了指向三个顶点的指针和指向通过三个边与其相邻的三个面的指针。如果面处于打开的网格的边界上,相应的邻接面的指针设为NULL。
三个邻接面的指针是这样被索引的:如果我们把从v到v[(i+1)%3]的边标记为第i个边,那么该边所对应的邻接面应该是f。这个标记约定要牢记住。以后当我们修正刚刚细分过的细分曲面的拓扑信息时,要用它来遍历整个网格。跟SDVertex相似,SDFace也存放指向下一级细分的子面的指针。
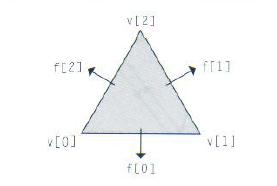
struct SDFace {
SDVertex *v[3];
SDFace *f[3];
SDFace *children[4];
};
SDFace构造器很简单,只是把变量都设为NULL。
为了简化对SDFace结构的遍历,我们提供了两个宏定义,用来确定某个顶点或面的前一个或后一个顶点或面的索引值。
#define NEXT(i) (((i+1)%3)
#define PREV(i) (((i+2)%3)
为了保证网格是流形网格(manifold mesh),LoopSubdiv要求网格是一致有序的(consistently ordered),也就是说每一个有向边只出现一次。一个被两个面共享的边要被声明两次,并且应该以相反的方向分别出现在两个面上。换个说法就是,所有的面上的顶点次序都是一致的:要么都是逆时针,要么都是顺时针:

一个反例是莫比乌斯带,它就不是一致有序的 【为了理解这一点,我们做一个莫比乌斯带: 用一个长纸条,在两端分别画上两个方向相反的箭头,如果将纸条拧一圈再将两端对接,就变成了莫比乌斯带,我们会发现两端的箭头是同向的–这跟我们的要求相反。】当然在实际应用中我们不会遇到这类的情况。但是,有些软件会生成不好的网格数据,从而引出麻烦。
有了以上对输入数据的假定,我们就可以在构造器中初始化网格的拓扑数据结构了。首先,构造器对所有的面进行遍历,把它们的三个v指针指向对应的三个顶点。同时,也将每个顶点的SDVertex::startFace指针指向顶点的某一个邻接面。具体指向那个邻接面并不重要,所以每次遇到顶点的邻接面就把它赋值给startFace,这样就可以保证在循环结束后,所有的顶点都有某个非空的面指针。
const int *vp = vertexIndices;
for(i = 0; i < nfaces; ++i) {
SDFace *f = faces;
for(int j = 0; j < 3; ++j) {
SDVertex *v = vertices[vp[j]];
f->v[j] = v;
v->startFace = f;
}
vp += 3;
}
我们还要把每个面的f指针指向它所对应的邻接面。这更复杂些,因为用户并没有提供面的邻接信息。构造器对所有的面进行遍历,为每条边创建一个SDEdge对象。当它遇到了共享同一条边的另一个面时,就把两个面的邻接面指针指向对方。
struct SDEdge {
SDVertex *v[2];
SDFace *f[2];
int f0edgeNum;
};
SDEdge构造器的参数是边的两个端点。它将两个端点排序,使得先在内存出现的顶点放在v[0]。这段代码有些奇怪,但它基于指针也是可以象整数那样可以比较的事实。排序的目的是保证边(va,vb)跟边(vb,va)会被视为同一个边。
SDEdge(SDVertex *v0 = NULL, SDVertex *v1 = NULL) {
v[0] = min(v0, v1);
v[1] = max(v0, v1);
f[0] = f[1] = NULL;
f0edgeNum = -1;
}
该类也定义了对SDEdge对象排序的操作,用来保证它们在其它数据结构中以定义好的顺序排列。
bool operator < (const SDEDge &e2) const {
if(v[0] == e2.v[0]) return v[1] < e2.v1[1];
return v[0] < e2.v[0];
}
现在构造器可以去做遍历所有面的工作了,在遍历过程中,设置每条边所对应的邻接面。它用了一个集合set来存放暂时只有一个邻接面的边。用set查找某条边的时间是O(log n)。
set
for(i = 0; i < nfaces; i++) {
SDFace *f = faces;
for (int edgeNum = 0; edgeNum < 3; ++edgeNum) {
}
}
对于每个面上的每条边,上面的循环体要创建一个SDEdge对象,看该边是否以前碰到过。如果是,则初始化和边对应的两个面的邻接面指针。否则,把它加入边的集合中。边的两个端点的索引值v0和v1,分别等于边索引值和边索引值加1。
int v0 = edgeNum, v1 = NEXT(edgeNum);
SDEdge e(f->v[v0], f->v[v1]);
if(edges.find(e) == edges.end()){
}
else {
}
如果该边以前没有遇到过,就把指向当前面的指针放在边对象的f[0]中。由于网格是流形网格,最多还有一个面共享这条边。发现了这个面后,就可以初始化其邻接面的指针了。我们把当前面的这条边的号码放在f0edgeNum中,这样它的邻接面就可以用这个号码初始化该面所对应的边的邻接面指针了。
e.f[0] = f;
e.f0edgeNum = edgeNum;
edges.insert(e);
当找到边的第二个面时,两个面的邻接面指针就可以设置为对方。这条边也可以删除了,因为没有两个以上的面共享同一条边。
e = *edges.find(e);
e.f[0] ->f[e.f0edgeNum] = f;
f->f[edgeNum] = e.f[0];
edges.erase(e);
现在所有面都设置好了邻接面指针,下面要设置每个顶点的boundary和regular标志。为了确定一个顶点是否为边界点,我们要定义围绕顶点的面的次序:对于面f的顶点v,我们定义顶点的“下一个面”为跟边( v, v[NEXT(i)] )相邻接的面, 定义顶点的“前一个面”为跟边( v[PREV(i)], v )相邻接的面。
不断地从一个面走到下一个面,我们就可以遍历顶点的邻接面。如果我们回到我们出发的面,这个顶点就是内部顶点;如果我们遇到一个NULL指针,则可断定它是边界顶点。然后再计算顶点的价,如果内部顶点的价为6或边界顶点的价为4,则为正规顶点,设regular为真;否则,它就是非正规顶点。
for(i = 0; i < nvertices; ++i) {
SDVertex *v = vertices;
SDFace *f = v->startFace;
do {
f = f->nextFace(v);
} while (f && f != v->startFace);
v->boundary = (f == NULL);
if(! v->boundary && v->valence() == 6)
v->regular = true;
else if( v->boundary && v->valence() == 4)
v->regular = true;
else
v->regular = false;
}
我们常常需要求顶点的价,其实现如下:
inline int SDVertex::valence() {
SDFace *f = startFace;
if (!boundary) {
} else {
}
为了计算非边界顶点的价,这个函数计算该顶点的邻接面个数,方法是跟着每个面的下一个面的指针走,直到抵达起始面为止,所遍历的面的个数就是顶点的价。
int nf = 1;
while((f = f->nextFace(this)) != startFace)
++nf;
return nf;
对于边界顶点,我们用同样的方法,但价是所遍历的面数加1。它的遍历方法有些复杂:首先沿着下一个面的指针走直到遇到NULL为止; 再从startFace开始沿着前一个面的指针走,直到遇到边界为止:
int nf = 1;
while((f = f->nextFace(this)) != NULL)
++nf;
f = startFace;
while((f = f->prevFace(this)) != NULL)
++nf;
return nf+1;
SDFace::vnum()是一个返回顶点指针的索引值的辅助函数。如果传入一个不是该面的顶点指针,则会发生严重错误–这种情况常常表明其它部分代码出现了错误。
int vnum(SDVertex *vert) const {
for (int i = 0; i < 3; i++)
if(v == vert) return i;
Severe(“Basic logic error in SDFace::vnum()”);
return -1;
}
因为面f上的顶点v的下一个面过第i条边,我们可以用辅助函数vnum()很容易地得到下一个面的指针。同样地,前一个面过边(PREV(i), i),用该函数也可以得到前一个面的指针:
SDFace *nextFace(SDVertex *vert) {
return f[vnum(vert)];
}
SDFace *prevFace(SDVertex *vert) {
return f[PREV(vnum(vert))];
}
我们也需要知道从任意一个顶点出发绕着面的下一个顶点或前一个顶点,所需函数如下:
SDVertex *nextVert(SDVertex *vert) {
return v[NEXT(vnum(vert))];
}
SDVertex *prevVert(SDVertex *vert) {
return v[PREV(vnum(vert))];
}
3.7.2 包围盒
Loop细分曲面具有凸包性质:极限曲面被包含在原控制网格的凸包中。所以,细分曲面的包围盒就是控制网格的包围盒,求法跟前面的TriangleMesh相同,这里就不提了。
3.7.3 细分
现在我们讲解如何用改进的Loop规则进行细分的。LoopSubdiv形体并不支持直接求交,而是通过固定次数的细分得到一个用来渲染的TriangleMesh。
bool LoopSubdiv::CanIntersect() const {
return false;
}
Refine()函数处理所有的细分过程。它对网格重复地使用细分规则,每一次细分都产生一个用于下一次细分的新网格。每一次细分后,Refine()函数要按照细分过的这级网格对f和v数组进行更改。当LoopSubdiv完成所有细分后,就创建好一个代表曲面的TriangleMesh并返回给调用者。第A.2.4节定义了ObjectArena类,用它可以快速地申请某个类型对象的内存空间,并当它超过其作用域时自动释放所申请的空间。
void LoopSubdiv::Refine(vector
vector
vector
ObjectArena
ObjectArena
for (int i = 0; i < nLevels; i ++ ) {
};
}
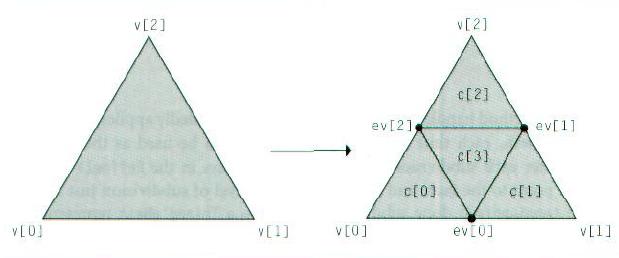
细分步骤中的主循环是这样进行的: 它为当前级的细分中所有的顶点和面创建vector,计算新的顶点位置,并更改细化的网格的拓扑数据。如图,每个面被分成4个子面,使得第i个子面紧挨着第i个顶点,而且最后一个子面处在中间位置。在原面上的三条边上,3个新的顶点被计算出来。
vector
vector
首先,要为那些已经在网格上的顶点申请内存空间(用于存放对原顶点的更改值)。同时,还要为子面申请内存。其中的初始化工作很少,只是设置顶点的regular和boundary标志值。注意细分后,原在边界上的顶点仍处于边界,在内部的顶点仍处于内部,且顶点的价保持不变。
for (u_int j = 0; j < v.size(); ++j) {
v[j]->child = new (vertexArena)SDVertex;
v[j]->child->regular = v[j]->regular;
v[j]->child->boundary = v[j]->boundary;
newVertices.push_back(v[j]->child);
}
for (u_int j = 0; j < f.size(); ++j)
for(int k = 0; k < 4; ++k) {
f[j]->children[k] = new (faceArena)SDFace;
newFaces.push_back(f[j]->children[k]);
}
计算新顶点的位置
在初始化细分网格的拓扑信息之前,先要计算所有顶点的位置。首先,要计算那些已经在网格上的顶点的新位置,这些顶点被称为偶顶点。然后,再计算在边上的新顶点,这些顶点被称为奇顶点。
不同类型的偶顶点要用不同的方法,这包括正规的,非正规的,边界上的,内部的情况。
for( u_int j = 0; j < v.size(); ++j) {
if(!v[j]->boundary) {
}
else {
}
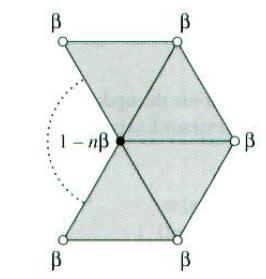
(见上图)对于内部的偶顶点(分正规、非正规两种),我们取跟它相邻的顶点的集合(称为一个绕着该顶点的一个环状集合:one-ring),并赋给每个集合中的顶点一个权值β。该顶点的权值设为1-nβ,其中n是顶点的价。这个顶点的新位置v’可由下面的公式计算出来:
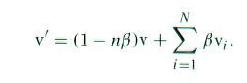
这个公式保证所有权值的和是1,这也保证了网格的凸包性。被修改的顶点位置只跟其附近的顶点相关,这就是所谓的局部支持性(local support)。Loop细分曲面的细分规则保证了这个性质,故应用广泛。
权值β是细分算法的关键,必须仔细地选择其值,从而保证极限曲面的平滑性。LoopSubdiv::beta()函数用顶点的价来计算β值。对于正规的内部顶点,LoopSubdiv::beta()返回1/16。因为这是个最常见的情形,我们就直接使用1/16,省去调用LoopSubdiv::beta()了。
if(v[j]->regular)
v[j]->child->P = weightOneRing(v[j], 1.f/16.f);
else
v[j]->child->P = weightOneRing(v[j], beta(v[j]->valence()));
static float beta(int valance) {
if(valence == 3) return 3.f / 16.f;
else return 3.f / (8.f * valence);
}
LoopSubdiv::weightOneRing()函数遍历顶点的邻接点,使用相应的权值计算顶点的新位置。 它用到了SDVertex::oneRing()函数,它返回围绕着该顶点的邻接点的位置。
Point LoopSubdiv::weightOneRing(SDVertex *vert, float beta) {
Point P = (1 – valence * beta) * vert->P;
for (int i = 0; i < valence; ++i)
P += beta *Pring;
return P;
}
由于邻接顶点的个数是可变的,我们用alloca()动态地申请空间:
int valence = vert->valence();
Point *Pring = (Point *)alloca(valence *sizeof(Point));
vert->oneRing(Pring);
oneRing()假定所传入的指针指向一个足够大的内存空间:
void SDVertex::oneRing(Point *p) {
if(!boundary) {
}
else {
}
}
取得内部顶点的邻接顶点环状集合(one-ring)相对容易一些,只需遍历跟顶点相邻的面,取中心顶点在每个邻接面的下一个顶点,并放入集合中。(用笔在纸上画一下就明白了)。
SDFace *face = startFace;
do {
*P++ = face->nextVert(this)->P;
face = face->nextFace(this);
} while(face != startFace);
取得边界顶点的邻接顶点环状集合(one-ring)要复杂一些。这里的实现小心地把环状集合(one-ring)放在给定的Point数组中,使得首尾两个数组元素是边界上两个邻接的顶点。这个次序很重要,因为邻接的边界顶点跟那些邻接的内部顶点相比,常常有不同的权值。所以我们要先遍历邻接面,直到遇见边界上的面为止(这样做的目的是找到真正的遍历开始位置),再沿另一个方向遍历,把所找到的点一个个地存放到数组里。
SDFace *face = startFace, *f2;
while ((f2 = face->nextFace(this)) != NULL)
face = f2;
*P++ = face->nextVert(this)->P;
do {
*P++ = face->prevVert(this)->P;
face = face->prevFace(this);
} while(face != NULL);
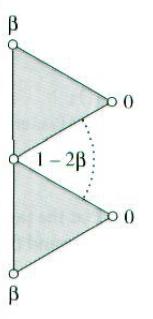
(见上图)对于边界上的点,顶点的新位置是基于两个边界上的邻接顶点来计算的。新位置不依赖于内部顶点保证了对于在边界上共用顶点的两个相邻接的细分曲面,它们的极限曲面也是相邻接的。weightBoundary()辅助函数利用两个邻近顶点v1和v2的权值,计算出顶点的新位置v’:
v’ = (1-2β)v + βv1+ βv2
正规的边界点和非正规的边界点都用权值1/8。
v[j]->child->P = weightBoundary(v[j], 1.f/8.f);
因为SDVertex::oneRing()把环状顶点集合(one-ring)的顶点排序,使得首尾两个数组元素是边界上两个邻接的顶点,这里的实现就更简单了。
Point LoopSubdiv::weightBoundary(SDVertex *vert, float beta) {
Point p = (1-2*beta) * vert->P;
P += beta *Pring[0];
P += beta *Pring[valence-1];
return P;
}
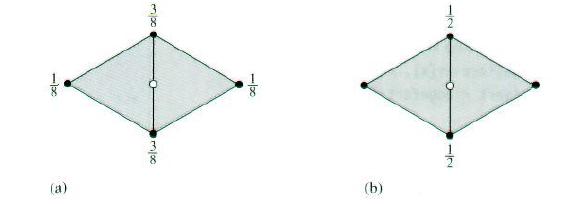
(见上图)我们现在计算奇顶点(即沿网格边上的顶点)的位置。首先,我们遍历网格中的每个面上的每条边,计算把边打断成两节的新顶点。对于内部边而言,我们取边的两个端点和与边相邻的两个面上的另外两个顶点,将这四个顶点的加权平均值作为新顶点。算法遍历每个面的三条边,每次发现一条新边,就为该边计算出新的奇顶点,再连同边一起存放关联数组edgeVerts中。
map
for(u_int j = 0; j < f.size(); j++) {
SDFace *face = f[j];
for(int k = 0; k < 3; ++k) {
}
}
SDEdge edge(face->v[k], face->v[NEXT(k)]);
SDVertex *vert = edgeVerts[edge];
if(!vert) {
edgeVerts[edge] = vert;
}
在Loop细分算法中,新添加的顶点总是正规的(这意味着随着细分级数的增加,非正规顶点和正规顶点的比例也降低了),所以新顶点的regular被设为true。boundary值也很容易初始化:只需检查被打断的边是否有邻接面。另外,新顶点的startFace指针也在这里被设置好。对于一个面上的所有奇顶点而言,处于中间的子面(面号码为3)总是跟新顶点相邻的。
vert = new (vertexArena) SDVertex;
newVertices.push_back(vert);
vert->regular = true;
vert->boundary = (face->f[k] == NULL);
vert->startFace = face->children[3];
对于边界奇顶点而言,新顶点是两个相邻的顶点的平均值。对于内部奇顶点而言,边上的两个端点的权值设为3/8,其它两个顶点的权值设为1/8,我们用SDFace::otherVert()辅助函数查找出这两个顶点。
if(vert->boundary) {
vert->P = 0.5f * edge.v[0]->P;
vert->P+ = 0.5f * edge.v[1]->P;
}
else {
vert->P = 3.f / 8.f * edge.v[0]->P;
vert->P += 3.f / 8.f * edge.v[1]->P;
vert->P += 1.f / 8.f * face->otherVert(edge.v[0], edge.v[1]) ->P;
vert->P += 1.f / 8.f *
face->f[k]->otherVert(edge.v[0], edge.v[1]) ->P;
}
SDFace::otherVert()的实现是一目了然的:
SDVertex *otherVert(SDVertex *v0, SDVertex *v1) {
for (int i = 0; i < 3; ++i)
if(v != v0 && v != v1)
return v;
Severe(“Basic logic error in SDVertex::otherVert()”);
return NULL;
}
修正网格拓扑信息
为了对网格拓扑修正算法的细节进行清楚简明的阐述,我们用下图所显示的编号规则。仔细地研究一下这个图吧,这里所用的表达方式对下面的几页描述至关重要。
为了修正细分过的网格的拓扑信息,有下面的4个主要任务:
1. 奇顶点的SDVertex::startFace指针要指向它的邻接面之一。
2. 同样地,偶顶点的SDVertex::startFace指针也要被设置好。
3. 新面的邻接面指针f要设置为相应的邻接面。
4. 新面的v要设置为相应的顶点。
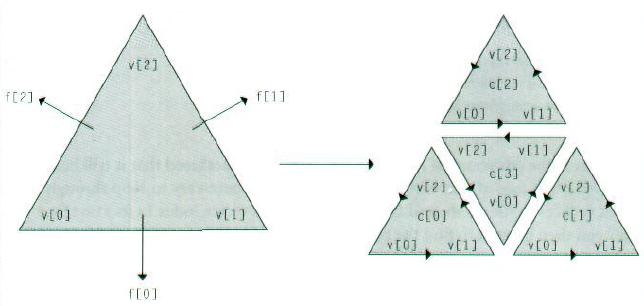
奇顶点的startFace指针已经在初始化时被设置好了,我们只需要处理其他三个任务。
如果顶点是其startFace的第i个顶点,那么可以保证它跟第i个子面的startFace邻接。所以,有必要遍历网格中所有的父顶点,对每个父顶点找到它在其startFace的顶点索引值。我们可以用这个索引值找到和新的偶顶点相邻的子面。
for (u_int j = 0; j < v.size(); ++j) {
SDVertex *vert = v[j];
int vertNum = vert->StartFace->vnum(vert);
vert->child->startFace =
vert->startFace->children[vertNum];
接下来,我们要修正新生成的面的邻接面指针。我们分两步进行:第一步,修正同一父面的子面的邻接面指针;第二步,修正不同父面的子面的邻接面指针。这里涉及了一些复杂的指针操作。
for(u_int j = 0; j < face.size(); ++j) {
SDFace *face = f[j];
for (int k = 0; k < 3; ++k) {
}
}
对于第一步,回忆一下,内部的子面存放在children[3]中。近一步地,第k+1个子面(k = 0,1,2)邻接内部子面的第k条边,而内部子面邻接第k个面的第k+1条边。
face->children[3]->f[k] = face->children[NEXT(k)];
face->children[k]->f[NEXT(k)] = face->children[3];
现在我们要修正另一类子面的邻接指针,它们指向其它父面的子面。我们只考虑前三个子面,因为第四个已经被初始化好了。好好研究一下上图,就会发现需要设置第k个子面的第k条边和第PREV(k)条边。为了设置k个子面的第k条边,我们要先找到父面的第k条边,然后找到共享这条边的(邻接子面的)父面f2。如果f2存在(表明它不在边界上),顶点v[k]的邻接子面的父面的索引值就算找到了。这个索引值就是我们要找的邻接子面的索引值。这一方法同样适用于条边和第PREV(k)条边所对应的子面。
SDFace *f2 = face->f[k];
face->children[k]->f[k] =
f2 ? f2->children[f2->vnum(face->v[k])] : NULL;
f2 = face->f[PREV(k)];
face->children[k]->f[PREV(k)] =
f2 ? f2->children[f2->vnum(face->v[k])] : NULL;
最后,我们完成修正拓扑信息的第四步:设置子面的顶点指针。
for(u_int j = 0; j < face.size(); ++j) {
SDFace *face = f[j];
for (int k = 0; k < 3; ++k) {
< Update child vertex pointers to new even vertex>
< Update child vertex pointers to new odd vertex>
}
}
对于第k个子面(k = 0,1,2),第k的顶点对应于和该子面相邻接的偶顶点。非内部的子面有一个偶顶点和两个奇顶点;内部的子面有三个偶顶点。这个顶点是父顶点child指针所指的顶点。
face->children[k]->v[k] = face->v[k]->child;
为了修正其余的顶点指针,我们又用到edgeVerts关联数组,用来寻找父面的每个边上的奇顶点。有三个子面共享该顶点,通过上图的编号规则,可以找到顶点在这三个子面中的索引值。
< Update child vertex pointers to new odd vertex> =
SDVertex *vert = edgeVerts[SDEdge(face->v[k], face->v[NEXT(k)])];
face->children[k]->v[NEXT(k)] = vert;
face->children[NEXT(k)]->v[k] = vert;
face->children[3]->v[k] = vert;
所有几何和拓扑方面的工作完成后,新创建的顶点和面被移到v和f数组。
f = newFaces;
v = newVertices;
求极限曲面上的点和输出
细分曲面的一个很好的性质就是有些特殊的细分规则可以给出极限曲面上的顶点。我们在这里使用这些规则来生成曲面上点的位置一个数组Plimit。在计算过程中把极限曲面上的点暂存在Plimit中而不是直接放在顶点数组,这一点很重要,因为每个顶点的极限曲面位置跟原顶点位置有关,所有顶点的原始位置在计算过程中不能改变。
对于边界顶点的极限规则是令相邻的两个顶点的权值为1/5,中心顶点的权值为3/5。内部顶点的极限规则是基于函数gamma(),它利用顶点的价来计算顶点适当的权值。
Point *Plimit = new Point[v.size()];
for(u_int i = 0; i < v.size(); i++) {
if(v->boundary)
Plimit = weightBoundary(v, 1.f/5.f);
else
Plimit = weightBoundary(v, gamma(v->valance())));
}
for(u_int i = 0; i < v.size(); i++)
v->P = Plimit;
static float gamma(int valence) {
return 1.f/(valence+3.f/(8.f * beta(valence)));
为了生成每个顶点带有曲面法向量的平滑的三角形网格,我们要在每个顶点上计算出两个极限曲面上的非平行的切向量。跟位置的极限规则相同,这里给出极限曲面上的精确的分析解。
vector
Ns.reserve(v.size());
int ringSize = 16;
Point *Pring = new Point[ringSize];
for(u_int i = 0; i < v.size(); i++) {
SDVertex *vert = v;
Vector S(0,0,0), T(0,0,0);
int valence = vert->valence();
if(valence > ringSize) {
ringSize = valence;
delete[] Pring;
Pring = new Point[ringSize];
}
vert->OneRing(Pring);
if(!vert->boundary)
else
Ns.push_back(Normal(Cross(S, T)));
}
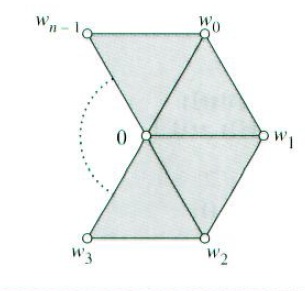
下图显示了计算网格内部的切向量的设置。中心的顶点的权值为零,相邻的顶点的权值设为wi。
当计算第一个切向量s时,权值是:
wi = cos(2πi / n)
其中n是顶点的价。当求第二个切向量t时,权值是:
wi = sin(2πi / n)
for(int k = 0; k < valence; ++k) {
S += cosf(2.f * M_PI * k/valence) * Vector(Pring[k]);
T += sinf(2.f * M_PI * k/valence) * Vector(Pring[k]);
}
求在边界上的顶点切向量有些麻烦,下图显示了环状顶点集合中顶点的顺序:
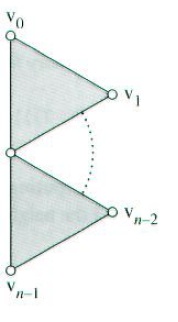
第一个切向量,又称对角切向量(across tangent),由v0和vn-1之间的向量给出:
s = vn-1 – v0
第二个切向量,又称横向切向量(transverse tangent),是根据顶点的价计算出来的。中心顶点的权值设为wc,而环状顶点集合的权由一个向量(w0, w1, …, wn-1)给出。下面为横向切向量的规则:
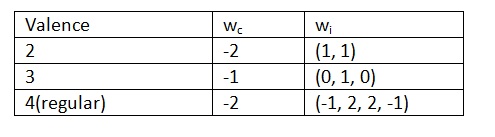
对于大于等于5的价, wc = 0, 并且:
w0 = wn-1 = sinθ
wi = (2cosθ – 2) sin(θi),
其中,θ = π /(n-1)
这里没有给出证明:对于所有i的值,它们的权的总和为零。这就保证加权和为切向量。
S = Pring[valence-1] – Pring[0];
if (valence == 2)
T = Vector(Pring[0] + Pring[1] – 2 * vert->P);
else if (valence == 3)
T = Pring[1] – vert->P;
else if (valence == 4)
T =Vector(-1 * Pring[0] + 2*Pring[1] + 2*Pring[2] +
– 1 *Pring[3] + -2 * vert->P);
else {
float theta = M_PI / float(valence -1);
T = Vector(sinf(theta) * (Pring[0] + Pring[valence-1]));
for (int k = 1; k < valence - 1; ++k) {
float wt = (2*cosf(theta)-2) * sinf((k) * theta);
T += Vector(wt * Pring[k]);
}
T = -T;
}
最后,片段
Categories: Garfield's Diary
