PBRT 几何和变换
第二章 几何和变换
几乎所有图形软件都以几何类(geometric classes, 这里指c++类)为基础.这些类表示了诸如点,向量,光线等等的数学构件. 由于我们在系统中会到处用到这些类, 良好的抽象和有效的实现至关重要. 本章会讲解pbrt的几何基础的接口和实现.
几何类见文件 core/geometry.h 和core/geometry.cpp.
变换矩阵见文件 core/transform.h 和core/transform.cpp.
2.1 坐标系统
pbrt用三个浮点数坐标值x,y,z来表示三维点,向量和法向量. 当然,这些值只有在一个给定的坐标系下才有意义: 给定一个原点和三个定义x,y,z轴的向量,就定义了这个坐标系(frame).
在n维空间中, 坐标系的原点P0和其n个线性无关的基向量定义了n维仿射空间(affine space).所有空间中的向量V可以被表达成为基向量(V1,V2, …, Vn)的线性组合:
V = s1V1 + s2V2 + … + snVn (s1, s2, … sn是唯一存在的一组纯量, 被称为V关于基(V1,V2…Vn)的表达).
同样地, 对与点P而言, 它可用原点P0和基向量(V1,V2, …, Vn)表达:
P = P0 + s1V1 + s2V2 + … + snVn
以上讨论有点循环定义的味道: 要定义坐标系我们需要定义一个点和一组向量, 而点和向量只有在给定的一个坐标系下才有意义. 因此,我们需要一个标准坐标系, 其原点是(0,0,0), 基向量为(1,0,0), (0,1,0) 和(0,0,1).
2.1.1 左/右手坐标系
我们知道坐标系分左手坐标系和右手坐标系,pbrt用左手坐标系.
2.2 向量
class COREDLL Vector {
public:
};
一个向量表达了三维空间内的一个方向, 它由三个浮点数定义:
float x, y, z;
x,y,z被定义为公共成员, 不太符合C++的封装原则, 但我们这样做是为了代码的清晰和效率.
缺省情况下, (x,y,z)被设成0. 用户可以选择给定任意值:
Vector(float _x = 0, float _y = 0, float _z = 0)
: x(_x), y(_y), z(_z) {
}
2.2.1 向量运算
向量加法运算:
Vector operator+(const Vector &v) const {
return Vector(x+v.x, y + v.y, z + v.z);
}
Vector& operator+=(const Vector &v) const {
x += v.x; y += v.y; z += v.z;
return *this;
}
向量减法运算与上类似, 略.
2.2.2 比例运算
比例运算是纯量乘法, 即是将向量每个分量乘以一个纯量, 从而改变了它的长度.
Vector operator*(float f) const {
return Vector(f*x, f*y, f*z);
}
Vector& operator*=(const Vector &v) const {
x *=f; y *= f; z *= f;
return *this;
}
inline Vector operator*(float f, const Vector &v) {
return v*f;
}
类似地,我们可以定义纯量除法 “operator/” 和 “operator /=”, 此略.
Vector类还有一个”取负值”的单操作符定义, 用来返回一个方向相反的向量:
Vector operator-() const {
return Vector(-x, -y, -z);
}
下面两个函数可以用索引值0,1,2方便地使用向量的各个分量: v[0]得到x值, v[1]得到y值, v[2]得到z值.
float operator[](int i) const {
Assert(i >= 0 && i <= 2);
return (& x);
}
float &operator[](int i) {
Assert(i >= 0 && i <= 2);
return (&x);
}
2.2.3 点积和叉积
对于两个向量V和W, 它们的点积(V . W)定义为: Vx*Wx + Vy*Wy + Vy*Wy.
inline float Dot(const Vector &v1, const Vector &v2) {
return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z;
}
点积跟两向量的夹角关系是:
(v.w) = |v| |w| cosθ
如果两个非退化(即非(0,0,0))的向量相互垂直, 则(v.w)为零; 反之,也成立. 两个或多个相互垂直的向量被称为是正交的(orthogonal), 一组正交的单位向量被称为规格化正交的(orthonormal).
假定u,v,w是向量, s是纯量, 则有下列性质:
(u . v) = (v . u)
(su . v) = s(v . u)
(u . (v + w)) = (u . v) + (u . w)
我们常常要计算点积的绝对值, 故有如下函数:
inline float AbsDot(const Vector &v1, const Vector &v2) {
return fabsf(Dot(v1,v2));
}
叉积是另一个很有用的向量操作. 给定三维空间的两个向量, 叉积v × w 是垂直于两者的向量. 注意这个新向量的朝向是由坐标系的左右手定则(handedness)决定的.给定两个正交的向量 v 和 w, 那么, (v, w, v × w) 就按照给定的左右手定则形成一个坐标系.
在左手系中, 叉积定义为:
(v × w)x = vy wz – vz wy
(v × w)y = vz wx – vx wz
(v × w)z = vx wy – vy wx
有一个帮助记忆的公式是计算下面矩阵的行列式值:
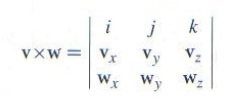
其中i, j, k分别代表轴(1, 0, 0), (0, 1, 0), (0, 0, 1). 注意这只是一个记忆工具, 而不是严格的数学表达, 因为矩阵把纯量和向量混合在一起用了.
inline Vector Cross(const Vector &v1, const Vector &v2) {
return Vector((v1.y * v2.z) – (v1.z * v2.y),
(v1.z * v2.x) – (v1.x * v2.z),
(v1.x* v2.y) – (v1.y * v2.z));
}
从叉积的定义中,我们得出:
| v × w | = | v | |w| sin θ (θ是v和w的夹角)
从上式可以看出, 两个相互垂直的单位向量的叉积也是一个单位向量. 如果两个向量平行, 则它们的叉积是个退化的向量. 另外, 可以看出, 以两个向量v1 , v2为边的平行四变形面积是| v1 × v2 |.
2.2.4 向量正规化
把一个向量变换成具有相同方向的单位向量就是向量的正规化, 方法是将向量的各个分量除以向量的长度:
float LengthSquared() const { return x * x + y * y + z * z;}
float Length() const { return sqrtf(LengthSquared());}
inline Vector Normalize (const Vector &v) {
Return v / v.Length();
}
2.2.5 由一个向量建立的坐标系
我们会经常用一个向量构造一个坐标系. 由于叉积跟两个向量垂直, 我们可以通过两次叉积(该向量跟任意一个向量叉积得到第二个向量, 第一和第二向量叉积得到第三个向量) 来得到三个相互垂直的向量,因而得到一个坐标系.
Pbrt所用的方法是: 给定一个正规化的向量v1, 把该向量其中一个分量置零并互换另外两个分量的值, 然后对之正规化,就得到第二个向量 v2 (可以验证v1和v2相互垂直), 再由v1和v2的叉积得到第三个向量:
inline void CoordinateSystem(const Vector &v1, Vector *v2, Vector *v3) {
if(fabsf(v1.x) > fabsf(v1.y)) {
Float invLen = 1.f/sqrtf(v1.x * v1.x + v1.z * v1.z);
*v2 = Vector(-v1.z * invLen, 0.f, v1.x * invLen);
}
else{
Float invLen = 1.f/sqrtf(v1.y * v1.y + v1.z * v1.z);
*v2 = Vector(0.f, v1.z * invLen, -v1.y* invLen);
}
*v3 = Cross(v1, *v2);
}
2.3 点
Class COREDLL Point {
Public:
};
点是三维空间的位置.虽然它跟向量一样也是用(x,y,z)三个坐标值表示, 但由于它们本质上的不同, 处理它们的方式也是不同的.
Float x, y, z;
跟Vector的构造器一样, Point构造器也是用可选的参数设置x,y,z的坐标值:
Point(float _x = 0, float _y = 0, float _z = 0)
: x(_x), y(_y), z(_z) {
}
有一些Point的函数返回一个Vector,或者用一个Vector作为参数. 比如, 把一个向量加到一个点上, 就是相当于将它在给定的方向上偏移而得到一个新的向量. 同样地, 两个点相减,得到它们之间的向量:
Point operator+ (const Vector &v) const {
return Point(x + v.x, y + v.y, z + v.z);
}
Point &operator += (const Vector &v) {
x += v.x; y += v.y; z += v.z;
return *this;
}
Vector operator- (const Point &p) const {
return Vector(x – p.x, y – p.y, z – p.z);
}
Point operator- (const Vector &v) const {
return Point(x – v.x, y – v.y, z – v.z);
}
Point &operator -= (const Vector &v) {
x -= v.x; y -= v.y; z -= v.z;
Return *this;
}
下面是求两点之间距离的函数:
inline float Distance(const Point &p1, const Point &p2) {
return (p1 – p2).Length();
}
inline float DistanceSquared(const Point &p1, const Point &p2) {
return (p1 – p2).LengthSquared();
}
虽然点乘以纯量不具数学意义, 但是Point类仍然支持纯量乘的定义, 用以求多个点的加权和. 其实现跟Vector中的实现类似, 从略.
2.4 法向量
class COREDLL Normal {
public:
};
法向量是在给定点上垂直于表面的向量。它可以被定义成两个互相不平行的表面切向量的叉积。虽然法向量跟向量很相似,但是应知它们的不同:因为法向量是根据它跟特定的曲面来定义的,在某些情况下跟向量是不同的,特别是使用变换的时候。(见第2.8节)。
Normal和Vector的实现很相似,都是用三个浮点数x,y,z表示,并定义了法向量之间的加,减,纯量乘,正规化等运算。但是,法向量不能跟一个点相加,也不能取两个法向量的叉积。还有,法向量不一定是正规化的。
Normal提供了由一个Vector初始化一个Normal的构造器。由于Normal和Vector有细微的差别,我们不希望它们之间有隐性的转换。为此,C++的explicit关键词可以保证它们之间显性的转换。
explict Normal(const Vector &v)
: x(v.x), y(v.y), z(v.z) {}
explict Vector(const Normal &n);
inline Vector::Vector(const Normal &n)
:x(n.x), y(n.y), z(n.z) { }
这样一来,如果声明了Vector v; Normal n; 那么 n = v 就是非法的,必须用显式的转换:n = Normal(v).
我们还重载了Dot()和AbsDot() 函数来覆盖求法向量和向量之间的求点积的各种组合情况, 另外,其它跟Vector类似的函数都不提及了。
2.5 光线
class COREDLL Ray {
public:
};
光线是一条由其原点和方向定义的射线。pbrt用Ray类来表达光线,其中用一个Point成员变量表示其原点,用一个Vector表示其方向:
Point o;
Vector d;
光线的参数化形式是一个关于纯量t的方程:
r(t) = o + t d 0 ≤t ≤ ∞
Ray类还包含两个值mint和maxt,把光线限定在[r(mint), r(maxt)]区间之间。 它们声明为mutable, 这意味着即使它们所在的Ray是const, 也是可以被改变的。其目的就是方便光线/物体的求交, 因为在这过程中,总是要记录最近的交点所对应的t值。
mutable float mint, maxt;
为了模拟运动模糊效果, 每条光线还需要一个时间值:
float time;
Ray的构造器很简单明了:
Ray() : mint(RAY_EPSILON), maxt(INFINITY), time(0.f) {}
Ray(const Point &origin, const Vector &direction,
float start = RAY_EPSION, float end = INFINITY, float t = 0.f)
: o(origin), d(direction), mint(start), maxt(end), time(t) {}
#define RAY_EPSILON 1e-3f
注意我们用一个极小的数(RAY_EPSILON)来初始化mint, 而不是用0, 原因是避免因浮点计算精度而引起的自相交的错误, 这是一个在光线追踪中的很典型的手法。
我们还重载函数操作符“()”, 来求和参数t对应的点:
Point operator() (float t) const { return o + d * t;}
这样,我们可以很方便地写类似下面的代码:
Ray r(Point(0,0,0), Vector(1,2,3));
Point p = r(1.7);
2.5.1 光线微分
为了更好地利用第11章定义的纹理函数进行反走样,pbrt对每条被追踪的光线都保持着一些附加的信息。 在第11.1节, 这些信息用在Texture类中估算一小部分的场景在图像平面上的投影面积。这样,Texture类就可以计算出纹理在这个面积上的平均值,从而得到更好的图像。
RayDifferential是Ray的子类, 并包含两条辅助光线的附加信息。 这两条光线表示从主光线向x和y方向分别偏置一个像素而得到的相机光线。确定了这三条光线投射到被着色物体上的区域,Texture就可以估算出用于反走样的平均值。
class COREDLL RayDifferential : public Ray {
public:
};
RayDifferential() { hasDifferentials = false;}
RayDifferential(const Point &org, const Vector &dir) : Ray(org, dir) {
hasDifferentials = false;
}
注意我们用到关键字explicit,防止不经意的Ray到RayDifferential的转换。 变量hasDifferentials被初始化为false, 表示相邻的两条光线还是未知的。
explicit RayDifferential(const Ray &ray) : Ray(ray) {
hasDifferentials = false;
}
bool hasDifferentials;
Ray rx, ry;
2.6 三维包围盒
class COREDLL BBOX {
public:
};
pbrt所要渲染的场景经常包含计算很费时的物体。 一个包含整个物体的三维包围体对很多操作而言都会非常有用。比如, 如果光线没有穿过包围盒, 就不必求光线和其中所包围的物体的交点了。
包围体的有效性跟两个因素有关:计算包围体的时间化费和包围盒包围物体的紧密程度。如果哦包围体太“宽松”了,就会浪费很多不必要的计算;反过来, 如果强求非常紧密的包围体,那么包围体很可能变得太复杂,时间耗费也会不菲。
包围体有很多种, pbrt用到沿轴的包围盒(axis-aligned bounding boxes, AABB). 其他的常见的选择包括沿方向的包围盒(oriented bounding boxes, OBB)和包围球。AABB可以由一个顶点和分别沿x,y,z轴方向的三个长度值来表示, 也可以由包围盒上两个相对的顶点来表示。pbrt就是用两点表示的,一个点的坐标是x,y,z的最小值,另一个是x,y,z的最大值。
BBOX缺省构造器把包围盒的范围定义成退化的 : pMin.x >pMax.x, 即是空包围盒。
BBox() {
pMin = Point (INFINITY, INFINITY, INFINITY);
pMax= Point (-INFINITY, -INFINITY, -INFINITY);
};
Point pMin, pMax;
有时我们用到包含一个点的包围盒:
BBox(const Point &p) : pMin(p), pMax(p) {}
我们还可以用两个点p1, p2来构造BBOX, p1和p2不必满足p1.x <= p2.x等条件, 构造器可以计算出最大、最小值:
BBox(const Point &p1,const Point &p2 ) {
pMin = Point(min(p1.x, p2.x), min(p1.y, p2.y), min(p1.z, p2.z));
pMax = Point(max(p1.x, p2.x), max(p1.y, p2.y), max(p1.z, p2.z));
}
给定一个包围盒和一个点,BBox::Union()计算并返回一个包含该点和原包围盒的新包围盒:
< BBox Method Definitions> =
COREDLL BBox Union(const BBOX &b, const Point &p) {
BBox ret = b;
ret.pMin.x = min(b.pMin.x, p.x);
ret.pMin.y = min(b.pMin.y, p.y);
ret.pMin.z = min(b.pMin.z, p.z);
ret.pMax.x = min(b.pMax.x, p.x);
ret.pMax.y = min(b.pMax.y, p.y);
ret.pMax.z = min(b.pMax.z, p.z);
return ret;
}
同样地,我们可以构造一个包含两个包围盒的包围盒:
friend COREDLL BBox Union(const BBox &b, const BBox &b2);
很容易判定两个包围盒是否重叠:
bool Overlaps(const BBox &b) {
bool x = (pMax.x >= b.pMin.x) && (pMin.x <= b.pMax.x);
bool y = (pMax.y >= b.pMin.y) && (pMin.y <= b.pMax.y);
bool z = (pMax.z >= b.pMin.z) && (pMin.z <= b.pMax.z);
return (x && y && z);
}
下面函数判定一个点是否在包围盒内:
bool Inside(const Point &pt) const {
return (pt.x >= pMin.x && pt.x <= pMax.x &&
pt.y >= pMin.y && pt.y<= pMax.y &&
pt.z >= pMin.z && pt.z<= pMax.z);
}
BBox::Expand()用来扩张包围盒, BBox::Volume()用来计算包围盒的体积:
void Expand(float delta) {
pMin -= Vector(delta, delta, delta);
pMax += Vector(delta, delta, delta);
}
float Volume() const{
Vector d = pMax – pMin;
return d.x * d.y * d.z;
}
BBox::MaximumExtent()返回最长的那个轴。在建造kd树时,我们用它决定沿那个轴划分。
int BBox::MaximumExtent() const {
Vector diag = pMax – pMin;
if (diag.x > diag.y && diag.x > diag.z)
return 0;
else if (diag.y > diag.z) return 1;
else return 2;
}
BBox::BoundingSphere()返回包含该包围盒的球的中心和半径。 虽然包围球比对应的包围盒要宽松得多, 但有时仍是很有用的。在第15章, 我们用它得到包含整个场景的包围球,用以生成可能跟场景相交的随机光线。
int BBox::BoundingSphere(Point *c, float *rad) const {
*c = 0.5f * pMin + 0.5*pMax;
*rad = Distance(*c, pMax);
}
Categories: Garfield's Diary
