PBRT 几何和变换 续
几何和变换 第2.7 – 2.9节
2.7 变换
一般地说, 变换T是从点到点或从向量到向量的映射:
p’ = T(p) v’ = T(v).
变换可以是任意的,但我们只考虑满足下面条件的变换:
1. 线性: 如果T是任意一个线性变换, s是任意纯量,那么 T(sv) = sT(v), T(v1+v2) = T(v1)+T(v2).这两个性质可以极大地简化变换的推导。
2. 连续性: 粗略地讲, T把p或v的邻近点或向量变换后,结果仍与p’或v’邻近。
3. 一一对应和可逆性:对每个点p, T把p映射到唯一的点p’.近一步地,存在可逆变换T-1把p’变换回p.
我们常常要计算一个点,向量或法向量在另一个坐标系下的坐标值。由线性代数中的知识可以知道,4乘4矩阵可以表达点或向量从一个坐标系到另一个坐标系的线性变换。另外,这样的4乘4矩阵可以表达同一坐标系下的所有关于点或向量的线性变换。所以,有下面关于矩阵的不同解释:
· 坐标系内的变换: 给定一个点,矩阵可以表达如何计算在同一坐标系下变换(比如平移)后的新点。
· 坐标系之间的变换: 一个矩阵可以表达在原坐标系下的点或向量在新坐标系下的坐标。
一般说来,变换可以让我们利用最方便的坐标系。举例来说,我们定义一个虚拟相机,它位于原点,朝向z轴,y轴指向上方,x轴指向右方。这可以极大地方便了相机的实现。然后,我们可以把相机放在场景的任何位置,令其朝向任何方向,我们只需定义一个变换,把在场景坐标系下的点映射到相机坐标系。
2.7.1 齐次坐标
给定有(p,v1,v2,v3)定义的坐标系,用(x,y,z)既可以表示点(Px,Py,Pz)也可以表示向量(Vx,Vy,Vz)。为了避免这两种表示的模糊性,我们利用本章开始介绍的点和向量的表达方式,把点写成内积形式[S1 S2 S3 1] [v1 v2 v3 P0]T, 把向量写成内积形式[S1′ S2′ S3′ 0] [v1 v2 v3 P0]T。[S1 S2 S3 1]被称为点的齐次表示,[S1′ S2′ S3′ 0] 被称为向量的齐次表示。第四个坐标值有时被称作权值。对于点而言,任何非零的纯量都可以做为权值:齐次点(1,3,-2,1)和(-2,-6,4,-2)代表同一个点(1,3,-2). 一般地说,齐次点和所表达的三维点有下列关系:
(x, y, z, w) = (x/w, y/w, z/w)
有了上面的基础,我们可以考察一个变换矩阵如何把点和向量变换到另一个坐标系的。设有矩阵M描述从一个坐标系到另一个坐标系的变换:

将M作用到x轴向量(1, 0, 0),有:
M [ 1 0 0 0]T = [m00 m10 m20 m30]T
所以,矩阵的四列就是变换下面的x,y,z轴和原点的结果:
x = [ 1 0 0 0]T
y = [ 0 1 0 0]T
z = [ 0 0 1 0]T
p = [ 0 0 0 1]T
我们不显式地使用齐次坐标,没有Homogeneous类。然而,下节定义的变换例程会隐式地把点,向量,法向量转换成齐次坐标形式,然后使用齐次坐标变换,再转换回三维坐标形式。这样,所有的齐次坐标处理都集中在一个地方(即在变换的实现中)。
class COREDLL Transform {
public:
private:
};
一个变换由一个对Matrix4x4对象的引用m来表示。底层的Matrix4x4定义在A.3.2节。m是以行为主(row-major)的形式存储的,就是说, 元素m[j]对应第i行,第j列的元素。为了方便,Transform类还保持了m的逆阵mInv.
使用引用计数的模版类Reference在A.2.2节中有所介绍。它自动记录有多少个对象保持对该对象的引用,并当引用计数为零时自动释放内存。
Transform类保持对矩阵的引用,而不是直接存储矩阵本身,这样多个Transform对象可以指向同一个矩阵。这意味着一个Transform的实例占很少的内存空间。如果场景中有非常多的形体,且拥有同一个物体/世界变换,那么它们都有自己的Transform对象,但是却共享同一个矩阵,这样所节省的空间是很可观的。
当然,这也会牺牲一些灵活性, 特别是矩阵一但建立就无法修改。在实际情况中,这不是问题,因为场景中的变换通常是当pbrt读场景描述文件时建立的,以后在渲染过程中也不需要修改。在这样的设计决定下,每次修改矩阵,都要创建一个新的矩阵。
Reference
2.7.2 基本操作
新变换被创建时,被初始化为单位变换:把点和向量映射到它自己的变换。这种变换用单位矩阵表示(即对角线上的元素都为1,而其它元素为0的矩阵)。
Transform() {
m = mInv = new Matrix4x4;
}
一个变换也可以由一个矩阵来初始化:
Transform(float mat[4][4]) {
m = new Matrix4x4(mat[0][0], mat[0][1], mat[0][2], mat[0][3],
mat[1][0], mat[1][1], mat[1][2], mat[1][3],
mat[2][0], mat[2][1], mat[2][2], mat[2][3],
mat[3][0], mat[3][1], mat[3][2], mat[3][3]);
mInv = m->Inverse();
}
Transform(const Reference
m = mat;
mInv = m->Inverse();
}
最后,我们给出最常用的Transform的构造器: 其参数是一个变换矩阵和已经计算好的逆阵。这种方法很不错,因为很多的几何变换的矩阵的逆阵是很简单的,我们就省去了计算逆阵的通用算法所产生的开销。当然,调用者要保证所提供的逆阵是正确的。
Transform(const Reference
const Reference
m = mat;
mInv = minv;
}
Transform GetInverse() const {
return Transform(mInv, m);
}
2.7.3 平移变换
平移变换是最简单的变换之一。对于点P,平移变换把点的坐标平移Δx, Δy, Δz, 记作T(Δx, Δy, Δz). 比如, T(2,2,1)(x,y,z) = (x+2, y+2, z+1). 平移变换有下列性质:
T(0,0,0) = I
T(x1,y1,z1) T(x2,y2,z2) = T(x1+x2, y1+y2, z1+z2)
T(x1,y1,z1) T(x2,y2,z2) = T(x2,y2,z2) T(x1,y1,z1)
T-1(x,y,z) = T(-x, -y, -z)
写成矩阵形式就是:
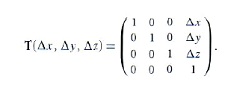
如果对点(x,y,z,1)进行平移变换,则有:
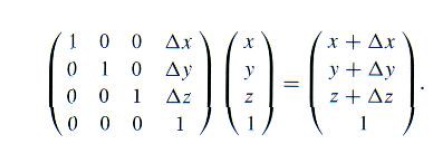
如果对向量(x,y,z,0)进行平移变换,则有:
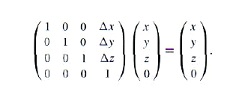
可以看出,平移的结果跟原向量相同,因为平移并不改变向量的方向,故也不改变向量的值。
平移变换的实现很简单:
COREDLL Transform Translate(const Vector &delta) {
Matrix4x4 *m, *minv;
m = new Matrix4x4(1, 0, 0, deltax,
0,1,0, deltay,
0,0,1,deltaz,
0,0,0,1);
mInv = new Matrix4x4(1, 0, 0, -deltax,
0,1,0, -deltay,
0,0,1,-deltaz,
0,0,0,1);
return Transform(m, minv);
}
2.7.4 比例变换
L另一个基本变换是比例变换, S(sx,sy,sz).其变换的结果等同于把点或向量的分量分别乘以比例因子. 比如: S(2, 2, 1)(x, y, z) = (2x, 2y, z).它有如下基本性质:
S(1, 1, 1) = I
S(x1, y1, z1) S(x2, y2, z2) = S(x1x1, y1y2, z1z2)
S-1(x,y,z) = S(1/x, 1/y, 1/z)
比例变换分等比例变换(uniform scaling, 三个比例因子相等), 和非等比例变换(nonuniform scaling, 三个比例因子不相等). 矩阵形式如下:
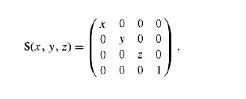
比例变换的实现很简单:
COREDLL Transform Scale(float x, float y, float z) {
Matrix4x4 *m, *minv;
m = new Matrix4x4( x, 0, 0, 0,
0, y, 0, 0,
0, 0, z, 0,
0, 0, 0, 1);
minv = new Matrix4x4(1.0f/x, 0, 0, 0,
0,1.0f/y,0, 0,
0,0,1.0f/z,0,
0,0,0,1);
return Transform(m, minv);
}
2.7.5 绕x,y,z轴的旋转变换
另一个变换类型是旋转变换R。一般地说,我们可以定义绕一个起始于原点的任意方向上的任意轴旋转任意角度的变换。最常用的变换还是绕x,y或z轴的变换,我们分别记为Rx(θ), Ry(θ), Rz(θ). 绕任意轴(x,y,z)旋转的变换记为R(x,y,z)( θ).
旋转变换的基本性质如下:
Ra(0) = I
Ra( θ1) Ra( θ2) = Ra( θ1 + θ2 )
Ra( θ1) Ra( θ2) = Ra( θ2) Ra(θ1 )
Ra-1(θ) = Ra(-θ) = RaT(θ)
其中RT是R的逆阵。最后一个性质表明旋转矩阵是正交矩阵: 逆阵等于其转置阵,其左上角3×3 所构成的三个向量是彼此正交的。
对于一个左手坐标系而言, 绕x轴旋转的变换矩阵是:
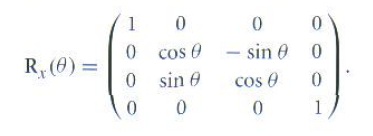
很容易得出它保持x轴不变,把y轴变换成(0, cos θ, sin θ), 把x轴变换成(0, -sin θ, cos θ).y轴和z轴旋转过给定角度后仍在同一平面中,且垂直于x轴。其实现如下:
COREDLL RotateX Scale(float angle) {
Float sin_t = sinf(Radians(angle));
Float cos_t = cosf(Radians(angle));
Matrix4x4 *m;
m = new Matrix4x4( 1, 0, 0, 0,
0, cos_t, -sin_t, 0,
0, sin_t, cos_t, 0,
0, 0, 0, 1);
return Transform(m, m->Transpose());
}
同样地, 绕y轴和绕z轴的变换矩阵分别是:
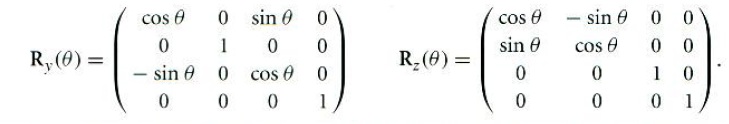
他们的实现从略。
2.7.6 绕任意轴的旋转变换
我们也提供一个计算绕任意轴的旋转变换的例程。这个矩阵的一般推导过程是把给定的任意轴映射到一个固定轴(如z轴),然后做旋转变换,再把固定轴变换到原来的任意轴上。我们这里给出一个更优美的向量代数推导。
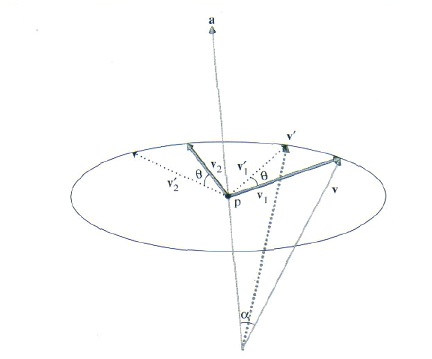
如图,考虑有任意轴,其方向的正规化向量是a, 向量v 绕该轴旋转角度θ。首先,我们计算过v的端点且跟向量a垂直的平面与向量a的交点p. 设v和a的夹角是α. 那么有:
|OP| = |v| cos α,
因为 v.a = |v| |a| cos α = |v| cos α, 则有:
p = |OP| a = a |v| cos α = a (v . a)
现在我们计算在这个平面上的两个基向量, 其中一个是现成的:
v1 = v – p
第二个可以取 a 和 v1的叉积:
v2 = (v1 X a)
因为a是正规化的向量, v1和v2长度相等,都等于从v到p的距离。设v在该平面上绕轴旋转θ后到达v’. 那么:
v’ = p + v1 cosθ + v2 sinθ
(则有: v’ = a(v.a) + (v- a(v.a)) cosθ + ((v- a(v.a)) X a) sinθ)
为了把这个公式转换成变换矩阵, 只需用之变换x,y,z轴, 即v分别取向量 (1,0,0), 0,1,0)和(0,0,1), 用上面的公式计算出矩阵上的左上角3×3个值。 我们可以从下面的实现中看出这个计算过程:
Transform Rotate(float angle, const Vector &axis) {
Vector a = Normalize(axis);
float s = sinf(Radians(angle));
float c = cosf(Radians(angle));
float m[4][4];
m[0][0] = a.x * a.x + (1.f – a.x * a.x) * c;
m[0][1] = a.x * a.y + (1.f – c) – a.z *s;
m[0][2] = a.x * a.z * (1.f – c) + a.y * s;
m[0][3] =0;
m[1][0] = a.x * a.y * (1.f – c) + a.z *s;
m[1][1] = a.y* a.y + (1.f – a.y * a.y) *c;
m[1][2] = a.y * a.z * (1.f – c) – a.x * s;
m[1][3] =0;
m[2][0] = a.x * a.z * (1.f – c) – a.y *s;
m[2][1] = a.y * a.z * (1.f – c) + a.x *s;
m[2][2] = a.z * a.z + (1.f – a.z * a.z) * c;
m[2][3] =0;
m[3][0] = 0;
m[3][1] = 0;
m[3][2] = 0;
m[3][3] =1;
Matrix4x4 *mat = new Matrix4x4(m);
return Transform(mat, mat->Transpose());
}
2.7.7 观察变换(Look-at Transformation)
观察变换用于把相机放置于场景之中: 使用者指定相机位置,朝向,和一个向上的向量(up vector)。这些值都是在世界坐标系中给出的。观察变换定义了相机空间和世界空间之间的变换。
为了求得变换矩阵, 我们仍应用前面介绍的原理:对三个坐标轴进行变换即得到矩阵的三个列向量。
Transform LookAt(const Point &pos, const Point &look, const Vector &up) {
float m[4][4];
Matrix4x4 *camToWorld = new Matrix4x4(m);
return Transform(camToWorld->Inverse(), camToWorld);
}
最容易求的是矩阵的第四列,因为它是把原点(0,0,0,1)进行变换后的结果,很清楚地,这就是用户所提供的相机位置。
m[0][3] = pos.x;
m[1][3] = pos.y;
m[2][3] = pos.z;
m[3][3] = 1;
求得其它三列的值也不那么困难。 首先, LookAt()计算从相机位置到观察点的正规化向量, 这就给出了z轴的变换结果, 也就是矩阵的第三列(在相机空间中,观察方向是沿+z轴的)。第一列是变换x轴的结果,是刚刚求得的观察方向的向量和用户所提供的向上向量的叉积。 最后,向上向量被重新计算–即取观察向量和x轴变换结果的叉积,这样保证三个向量是彼此正交的。
Vector dir = Normalize(look – pos);
Vector right = Cross(dir, Normalize(up));
Vector newUp = Cross(right, dir);
m[0][0] = right.x;
m[1][0] = right.y;
m[2][0] = right.z;
m[3][0] = 0;
m[0][1] = newup.x;
m[1][1] = newup.y;
m[2][1] = newup.z;
m[3][1] = 0;
m[0][2] = dir.x;
m[1][2] = dir.y;
m[2][2] = dir.z;
m[3][2] = 0;
2.8 变换的应用
现在我们定义对点或向量实施变换的一系列例程。我们将重载函数应用操作符”()”, 这样我们可以写类似下面的代码:
Point P = …;
Transform T = …;
Point new_P = T(P);
2.8.1 点
点的变换例程把点(x,y,z)隐性地表示为齐次列向量(x,y,z,1), 然后用矩阵乘以该向量。最后,结果除以w,变换回非齐次向量的表示。为了效率,当w=1时,就跳过这个除以w的步骤 –绝大多数情况下是这样的, 只有第六章定义的投影变换需要这个除法。
inline Point Transform::operator() (const Point &pt) const {
float x = pt.x, y = pt.y, z = pt.z;
float xp = m->m[0][0]*x + m->m[0][1]*y + m->m[0][2]*z + m->m[0][3];
float yp = m->m[1][0]*x + m->m[1][1]*y + m->m[1][2]*z + m->m[1][3];
float zp = m->m[2][0]*x + m->m[2][1]*y + m->m[2][2]*z + m->m[2][3];
float wp = m->m[3][0]*x + m->m[3][1]*y + m->m[3][2]*z + m->m[3][3];
Asssert(wp != 0);
if(wp == 1.) return Point(xp, yp, zp);
else return Point(xp,yp,zp)/wp;
}
我们还提供让调用者传入指向结果的指针的变换函数,这会省去返回栈上值的开销。注意我们把原(x,y,z)坐标值拷贝到局部变量,这样就允许指向结果的指针指向pt本身。
inline void Transform::operator() (const Point &pt, Point *ptrans) const {
float x = pt.x, y = pt.y, z = pt.z;
ptrans->x = m->m[0][0]*x + m->m[0][1]*y + m->m[0][2]*z + m->m[0][3];
ptrans->y = m->m[1][0]*x + m->m[1][1]*y + m->m[1][2]*z + m->m[1][3];
ptrans->z = m->m[2][0]*x + m->m[2][1]*y + m->m[2][2]*z + m->m[2][3];
float w = m->m[3][0]*x + m->m[3][1]*y + m->m[3][2]*z + m->m[3][3];
if(w != 1.) *ptrans /= w;
}
2.8.2 向量
向量的变换运算跟前面的很相似,但由于向量的w值是0, 计算有所简化。
inline Vector Transform::operator() (const Vector &v) const {
float x = v.x, y = v.y, z = v.z;
return Vector(m->m[0][0]*x + m->m[0][1]*y + m->m[0][2]*z,
m->m[1][0]*x + m->m[1][1]*y + m->m[1][2]*,
m->m[2][0]*x + m->m[2][1]*y + m->m[2][2]*);
}
同样地,也有一个传入结果指针的向量变换函数,这里就从略了。
2.8.3 法向量
对法向量进行变换不能同向量一样(否则变换后的法向量不再垂直于表面)。由于法向量n跟任意切向量t是正交的,我们有:
n . t = n T t = 0
当我们用矩阵M对点进行变换时,新的切向量t’所在的变换后所得到的点是Mt. 被变换后的法向量n’应该等于某个4×4矩阵S乘以n :
n’ = S n
为了保证正交性,必定有:
0 = (n’)T t’ = (S n)T M t = nT ST Mt
可以看出,当STM = I(单位矩阵)时,上式成立。 所以, S = (M-1)T。这表明我们必须用变换矩阵的逆阵的转置阵来对法向量进行变换,这也是我们必须在Transform类中保持逆阵的原因。
inline Normal Transform::operator() (const Normal &n) const {
float x = n.x, y = n.y, z = n.z;
return Normal(mInv->m[0][0] *x + mInv->m[1][0]*y + mInv->m[0][0]*z,
mInv->m[0][1] *x + mInv->m[1][1]*y + mInv->m[0][1]*z,
mInv->m[0][2] *x + mInv->m[1][2]*y + mInv->m[0][2]*z);
}
2.8.4 光线
对光线变换很简单: 只需变换原点和方向,并拷贝其它的数据成员:
inline Ray Transform::operator() (const Ray &r) const {
Ray ret;
(*this)(r.0, &ret.o);
(*this)(r.d, &ret.d);
ret.mint = r.mint;
ret.maxt = r.maxt;
ret.time = r.time;
return ret;
}
2.8.5 包围盒
变换包围盒最容易的方法是变换所有8个顶点,然后计算包含这8个变换后的顶点的包围盒。
BBOX Transform::operator() (const BBox &b) const {
const Transform &M = *this;
BBOX ret( M(Point(b.pMin.x, b.pMin.y, b.pMin.z)));
ret = Union(ret, M(Point(b.pMax.x, b.pMin.y, b.pMin.z)));
ret = Union(ret, M(Point(b.pMin.x, b.pMax.y, b.pMin.z)));
ret = Union(ret, M(Point(b.pMin.x, b.pMin.y, b.pMax.z)));
ret = Union(ret, M(Point(b.pMin.x, b.pMax.y, b.pMax.z)));
ret = Union(ret, M(Point(b.pMax.x, b.pMin.y, b.pMin.z)));
ret = Union(ret, M(Point(b.pMax.x, b.pMax.y, b.pMin.z)));
ret = Union(ret, M(Point(b.pMax.x, b.pMin.y, b.pMax.z)));
ret = Union(ret, M(Point(b.pMax.x, b.pMax.y, b.pMax.z)));
return ret;
}
2.8.6 复合变换
考虑一组复合变换ABC,其对点p的变换相当于 A(B(C(p))) = T(p). 我们可以写成:
Transform T = A * B * C;
为此,我们用C++ “*”操作符来定义复合变换,即矩阵的乘法。为了求得复合变换的逆阵,我们用到:
(AB)-1 = B-1A-1.
Transform Transform::operator *(const Transform &t2) const {
Reference
Reference
return Transform(m1,m2);
}
2.8.7 变换和坐标系的左右手定则(Handedness, 又称“手性”)
有些类型的变换把左手系变换成右手系,反之也是。有些例程需要知道需要知道变换是否产生了这种改变。特别是那些要保证表面法向量保持指向“外面”的例程,当这种改变发生时,需要把法向量的方向反转过来。
幸运地是,很容易得知一个变换能否改变坐标系的手性: 只需看其左上角3×3子阵的行列式值是否小于零。
bool Transform::SwapsHandedness() const {
float det = (( m->m[0][0] *
(m->m[1][1] * m->m[2][2] –
m->m[1][2] * m->m[2][1])) –
(m->m[0][1] *
(m->m[1][0] * m->m[2][2] –
m->m[1][2] * m->m[2][0])) +
(m->m[0][2] *
(m->m[1][0] * m->m[2][1] –
m->m[1][1] * m->m[2][0])));
return def < 0.f;
}
2.9 微分几何
在本章的结束,我们介绍一个对表面上点(特别是光线跟表面的交点)的自成一体的几何描述。这种抽象需要隐藏点所在的形体的类型,却能提供关于该点的足够信息用以着色和几何操作,而无需关心不同形体类型的区别(如球,三角形等)。DifferentialGeometry类就是实现了这种抽象。其中包括:
· 三维点p的位置。
· 该点的法向量n。
· 曲面参数形式下的(u,v)坐标值。
· 参数化的偏导数 dp/ du, dp/ dv。
· 关于法向量变化的偏导数 dn/ du, dn/ dv。
· 一个指向点所在的形体(Shape)的指针。
这个表达假定形体有参数化的描述 – 即对于某个范围内的(u,v)值,有曲面上的点p = f(u,v)与之对应。
Point p;
Normal nn;
float u, v;
const Shape *shape;
我们也定义关于曲面位置和法向量的偏导数:
Vector dpdu, dpdv;
Vector dndu, dndv;
它的构造器如下:
DifferentialGeometry:: DifferentialGeometry(const Point &p,
const Vector &DPDU, const Vector &DPDV,
const Vector &DNDU, const Vector &DNDV,
float uu, float vv, const Shape *sh)
:p(P), dpdu(DPDU), dpdv(DPDV), dndu(DNDU), dndv(DNDV) {
}
nn = Normal(Normalize(Cross(dpdu, dpdv)));
u = uu;
v = vv;
shape = sh;
表面法向量对于pbrt而言有特殊的含义, 即假定: 对于封闭的形体,法向量总是指向形体的“外面”。例如,这个假设会在我们决定光线是进入还是离开形体的时候会用到。另外,对于那些作为面光源的形体而言,只有法向量所在的表面那一面才是发光的,而另一面是没有光的。
正是由于这一点,pbrt提供一个机制,用户可以用以反转法向量的方向,使之指向相反的方向。在pbrt输入文件中,有ReverseOrientation指令用来反转法向量。所以,有必要检查所给定的形体Shape中的这个标志, 如果该标志被设置了,就要反转法向量。
另外,有另一个因素也影响法向量的朝向, 即Shape的变换是否改变物体坐标系的手性(Handedness)。(容易举出这样的例子,比如比例变换:S(1, 1, -1))。
所以,当以上两个条件只有一个被满足,则需反转法向量。如果两者都满足,则它们的效应相互抵消了,无需反转法向量。可见,这是一个XOR操作:
if( shape->reverseOrientation ^ shape->transformSwapsHandedness)
nn *= -1.f;
Categories: Garfield's Diary
