PBRT 体素和求交加速
第4章 体素和求交加速
上一章所介绍的类专注于如何表达3D物体的几何性质。虽然Shape类对于象求交和求包围盒之类的几何操作是很方便的抽象,但它并不包括描述一个场景中物体的足够的信息。例如,我们必须把材质信息和形体加在一起才可以说明形体的外观。为了达到这些目标,本章介绍Primitive类及其几个实现。
直接用来渲染的形体用GeometricPrimitive类来表达。这个类把一个Shape和关于其外观性质的描述结合起来。这样做的目的是把pbrt的几何部分和渲染部分清楚地分离开来,这些外观性质被封装在Material类中,具体见第10章。
有些场景包含许多同一个体素在不同位置上的拷贝。对关联拷贝(instancing)的支持可以极大地减少场景对内存的需求,因为每一个拷贝只存放对体素的指针和一个变换。为此,pbrt提供了InstancePrimitive类。每一个InstancePrimitive对象有一个单独的变换用来把它放置在场景之中,但可以同其它InstancePrimitive对象共享同一个体素。
本章还将介绍Aggregate基类,它表示一个可以包含许多Primitive的容器(container)。pbrt用这个类来实现加速结构–这是一个数据结构,它可以降低场景中n个物体和光线求交测试的复杂性。大多数光线只跟很少的体素相交。如果一个加速结构一次可以排除一组体素,那么这跟必须测试每个体素的情况相比较,将会有实质性的性能提升。这些加速结构重用了Primitive接口(加速结构是Aggregate的子类,而Aggregate也是Primitive的子类),这样做的好处是pbrt可以支持混合形的加速方法,也就是说一个类型的加速结构可以包含其它类型的加速结构。
本章介绍两种加速结构:GridAccel结构,它基于一个覆盖场景的均匀网格;另一个是KdTreeAccel,它基于自适应递归式空间划分(adaptive recursive spatial subdivision)。
4.1 Primitive接口和几何体素
抽象基类Primitive是pbrt几何处理子系统和着色子系统的桥梁。它继承了ReferenceCounted基类,可以自动地记录对象引用次数,当最后一个引用脱离作用域时,就释放对象所占用的内存。含有Primitive的其它的类不应该存放Primitive的指针,而应存放Reference
class COREDLL Primitive : public ReferenceCounted {
public:
};
因为Primitive类把几何操作和着色操作联系起来,它的接口也包括跟两者有关的函数。它有5个几何例程,它们都和Shape类中的函数很相似。第一个是Primitive::WorldBound(),返回体素在世界空间的包围盒。包围盒有很多用途,其中最重要的一个用途是用于把Primitive放入加速结构的过程中。
virtual BBox WorldBound() const = 0;
跟Shape类相似,所有的Primitive都能够决定是否可以直接求光线跟体素的交点,如果不能,还要能够把它细分成一个或多个新的primitive。跟Shape相似,Primitive有一个函数Primitive::CanIntersect(),用来决定它的体素是否可以直接求交点。
跟Shape接口的一个不同之处是,Primitive求交函数返回一个Intersection结构,而不是一个DifferentialGeometry结构。这些Intersection结构除了包括交点的局部几何信息外,还有诸如材料性质等其它信息。
另一个不同是Shape::Intersect()只返回沿光线上到交点的参数距离,而Primitive::Intersect()还要更改光线的Ray::maxt值。这样做的好处是上一章所介绍的几何例程没必要关心系统的其它部分如何使用这个参数距离。
virtual bool CanIntersect() const ;
virtual bool Intersect(const Ray &r, Intersection *in) const = 0;
virtual bool Intersect (const Ray &r) const = 0 ;
virtual void Refine(vector
Intersection结构包含关于光线和体素交点的信息,包括点在表面上的微分几何信息,指向Primitive的指针,还要一个世界空间到物体空间的变换。
struct COREDLL Intersection {
DifferentialGeometry dg;
const Primitive *primitive;
Transform WorldToObject;
};
有时候我们需要不断地细化一个体素,直到所返回的新体素都可以求交为止。Primitive::FullyRefine()就是做这项工作的。它的实现很简单。它保持一个要细化的Primitive队列(todo队列),然后不断地从队列中取出Primitive,对之调用Primitive::Refine()。由Primitive::Refine()返回的那些可求交的体素被加入到输出队列中,而不可求交的体素被到todo队列中,这样一直处理下去,直到todo队列空为止。
void FullyRefine(vector
void Primitive ::FullyRefine(vector
vector
todo.push_back(const_cast
while(todo.size()){
}
}
Reference
todo.pop_back();
if(prim->CanIntersect())
refined.push_back(prim);
else
prim->Refine(todo);
除了几何操作函数以外,Primitive还有两个跟材料性质相关的函数。第一个是Primitive::GetAreaLight(),它返回一个指向AreaLight的指针,AreaLight类用来描述体素(如果它本身是光源的话)的发射光分布。
另一个函数是Primitive::GetBSDF(),返回一个BSDF指针(见第10.1节)。BSDF用来描述表面上的点的光散射的材料性质。该函数的参数是交点处的微分几何信息,和一个世界空间到物体空间的变换。这个变换将会后面讲的InstancePrimitive类中用到。
virtual const AreaLight *GetAreaLight() const = 0;
virtual BSDF *GetBSDF(const DifferentialGeometry &dg, const Transform &WorldToObject)
const = 0;
4.1.1 几何体素(Geometric Primitives)
GeometricPrimitive类用来表示场景中的单个的形体(如一个球)。对于用户所提供的场景描述文件中的每个形体,pbrt都会为它创建一个GeometricPrimitive对象。
class GeometricPrimitive : public Primitive {
public:
private:
}
每个GeometricPrimitive都保存一个对Shape的引用和Material的引用。另外,由于pbrt中的体素可以是面光源,它还有一个指向描述发光特性的AreaLight的指针(如果体素不发光,则设为NULL)。
Reference
Reference
AreaLight *areaLight;
GeometricPrimitive的构造器初始化这些变量,这里就不列出具体实现了。
GeometricPrimitive(const Reference
const Reference
AreaLight *a);
Primitive接口中和几何处理相关的大多数函数只是调用Shape中相应的函数而已。例如,GeometricPrimitive::Intersect()调用Shape::Intersect()来做实际的几何求交运算,再用所得到的交点初始化一个Intersection对象。还有,它还要把Ray::maxt的成员更新为所返回的交点参数距离。这样把最近的交点参数距离保存在Ray::maxt的主要好处是,如果发现体素处于光线的给定范围(mint,maxt)之外,就不必做进一步的求交测试了。
< GeometricPrimitive Method Definitions> =
bool GeometricPrimitive::Intersect(const Ray &r, Intersection *isect) const {
float thit;
if(!shape->Intersect(r, &thit, &isect->dg))
return false;
isect->primitive = this;
isect->WorldToObject = shape->WorldToObject;
r.maxt = thit;
return true;
}
我们不再把GeometricPrimitive的WorldBound(), IntersectP(), CanIntersect(), Refine()函数的实现列在这里,它们只是调用Shape类中相应的函数而已。类似地,GetAreaLight()只是返回GeometricPrimitive::areaLight成员变量。
最后,GetBSDF()函数调用Shape中的函数求得着色信息,并用Material中的函数计算BSDF值。
< GeometricPrimitive Method Definitions> +=
BSDF * GeometricPrimitive::GetBSDF(const DifferentialGeometry &dg,
const Transform &WorldToObject) const {
DifferentialGeometry dgs;
shape->GetShadingGeometry(WorldToObject.GetInverse(), dg, &dgs);
return material->GetBSDF(dg, dgs);
4.1.2 物体关联拷贝(Object Instancing)
物体关联拷贝是一项很经典的技术:一个体素可以被变换到场景中的多个位置中。例如,一个音乐厅的模型包括几千个相同的座位,如果所有的座位都使用同一个座位的几何表示,那么场景描述文件可以被大大地压缩。图4.1中的生态场景有4000颗不同类型的植物,而植物模型只有61个。因为用了关联拷贝,虽然整个场景有19.5百万个三角形,但内存只存了1.1百万个三角形。pbrt在渲染过程中用了大约300MB的内存。
物体关联拷贝是由InstancePrimitve类处理的。它有一个对被共享的Primitive的引用,一个实例到世界空间(instance-to-world-space)的变换,用来把它放置到场景中。如果要一次关联拷贝多个Primitive,就要把它们放在一个聚合体(Aggregate)对象中,这样就需只存一个Primitive对象了。
InstancePrimitive要求其中的Primitive是可以求交的,否则对每个拷贝进行细化就太耗时间和内存了。请参见第B.3.6节中的pbrtObjectInstance()代码,它根据场景描述文件创建关联拷贝,并细化,创建聚合体(aggregate)对象等等。
class InstancePrimitive : public Primitive {
public:
< InstancePrimitive Public Methods>
private:
< InstancePrimitive Private Data>
};
< InstancePrimitive Public Methods> =
InstancePrimitive(Reference
instance = i;
InstanceToWorld = i2w;
WorldToInstance = i2w.GetInverse();
}
< InstancePrimitive Private Data> =
Reference
Transform InstanceToWorld, WorldToInstance;
InstancePrimitive的核心任务是协调它所实现的Primitive接口和它所包含的Primitive的工作,并负责对它所包含的变换矩阵的使用。InstancePrimitive的WordToInstance变换定义了该拷贝所共享的体素的从世界到该拷贝的坐标系的变换。该拷贝中的共享体素有它自己的变换,这个变换应该被视为从InstancePrimitive的坐标系到物体空间的变换。整个到世界空间的变换需要这两个变换共同完成。
这样,InstancePrimitive::Intersect()函数把给定的光线变换到共享体素的坐标系中,并把被变换过的光线传给Intersect()函数。如果找到了交点,交点处的DifferentialGeometry要被变换到世界空间。这个任务由片段
bool InstancePrimitive::Intersect(const Ray &r, Intersection *isect) const {
Ray ray = WorldToInstance(r);
if(!instance->Intersect(ray, isect))
return false;
r.maxt = ray.maxt;
isect->WorldToObject = isect->WorldToObject * WorldToInstance;
< Transform instance's differential geometry to world space>
return true;
}
其它的有关几何操作的Primitive函数只是把调用传给共享的拷贝,结果要用InstancePrimitive的变换做相应的变换。
BBox WorldBound() const {
return InstanceToWorld(instance->WorldBound());
}
InstancePrimitive::GetAreaLight()和InstancePrimitive()::GetBSDF()是不会被调用的。对相应函数的调用应该是对和光线相交的体素进行的。对InstancePrimitive的这些函数的调用会产生运行时错误。
4.2 聚合体(Aggregates)
聚合体结构是任何光线追踪程序的核心组件之一。如果不减少不必要的光线求交测试,追踪一条穿过场景的光线所花费的时间跟场景中体素的个数成线性关系,因为光线为了求得最近交点,要和每个体素进行交点测试。这样做是极为耗时的,因为在大多数场景中,光线跟绝大多数的体素没有交点。加速结构的目的就是可以快速地排除成组的体素,同时使搜索过程按一定的顺序进行,尽量先求得近一些的交点,这样远一些交点的求交过程就有可能被跳过去。
因为在光线追踪程序中光线-物体求交占了大量的运行时间,所以有大量的有关求交加速算法的研究。这里就不探讨太多的内容了。
广泛地说,有两类解决问题的方法:空间划分算法和物体划分算法。空间划分算法把三维空间分解成区域(例如,在场景中加上轴对齐的网格),并记录下哪一个体素和哪些区域有重叠。在有些算法中,区域还可以根据相重叠的体素个数再进一步地做自适应性的划分。在求光线交点时,只有光线穿过的区域才会被考虑,并且只有跟这些区域重叠的体素才会和光线做交点测试。
与之相对应的另一个方法是物体划分,它把场景中的物体分成更小的组成部分。例如,一个房间模型可以被分成4面墙,一个屋顶,一把椅子。如果光线和房间的包围盒不相交,那么整个房间中的体素就被剔除了。否则,光线跟每一个物体进行测试。如果光线跟椅子的包围盒相交,则要测试它的椅子腿、座子,靠背;否则,整把椅子被剔除出去。
这两种方法对光线求交的计算加速都很成功,但没有任何理由说一个会比另一个好。本章所介绍的GridAccel和KdTreeAccel都是基于空间划分的。
Aggregate类提供了一个把多个物体归为一组的接口。因为Aggregate本身实现了Primitive接口, pbrt不需要为加速提供特殊的支持。Integrator可以写成象单个的体素一样,可以进行交点检查而无需关心交点是如何求得的。更进一步地,为了试验新的加速技术,只需写一个新的Aggregate体素,并加到pbrt中来。
class COREDLL Aggregate : public Primitive {
public:
};
跟InstancePrimitive类似,Aggregate求交例程 把Intersection::primitive指针指向实际跟光线相交的那个体素,而不是包含那个体素的聚合体。因为pbrt用这个指针取得交点上的信息(如反射性质,发射光性质等),我们绝不会去调用Aggregate::GetAreaLight()和Aggregate::GetBSDF()函数,而它们的实现只是返回运行时错误。
4.2.1 光线和盒子的求交
下面所介绍的GridAccel和KdTreeAccel都有一个包围盒BBox来包围其中所有的体素。这个包围盒可以用来判定光线是否跟其中某个体素相交;如果光线跟盒子没有相交,那么光线也不会跟盒子里的任何一个体素有交点。进一步地,这两种加速方法都用光线进入盒子的入点和离开盒子的出点作为其遍历算法的输入的一部分。因此,我们加一个BBox::IntersectP()函数,用来做光线-盒子的交点检查,如果有交点,则返回两个交点的参数t值。
我们可以把包围盒看成三个平板(slab)所构成的交集,一个平板是两个平行平面所构成的中间区域。为了求光线跟盒子的交点,只需逐个地求光线和这三个平板的交点。如果平板是和三个坐标轴对齐的,就可以做几个光线-平板求交的优化。
光线-包围盒求交算法基本上是这样工作的:我们从光线上的一段能覆盖交点的参数区间开始,比如说[0,无穷大 ),作为当前的包围盒的参数区间,然后我们逐步地计算光线和每个平板的交点的两个参数t值,所得到的参数区间都跟包围盒当前的区间求交集。如果交集是退化的,则没有交点。如果三个平板的区间都通过交集计算而得到非退化的区间,那么我们就得到了光线在盒子里的参数范围。下图演示了这个过程。
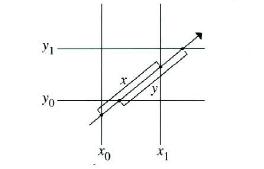
下图显示了光线和平板之间的几何关系。
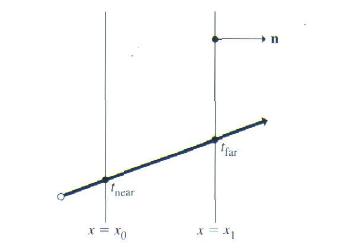
如果BBox::IntersectP()返回真,交点的参数范围被放在可选的变量hitt0,hitt1中。落在Ray::mint/Ray::maxt范围之外的交点会被舍去。如果光线起始位置ray(ray.mint)是在包围盒之内,则把ray.mint的值返回给hitt0。
bool BBox::IntersectP(const Ray &ray, float *hitt0, float *hitt1) const {
float t0 = ray.mint, t1 = ray.maxt;
for (int i = 0; i < 3; ++i) {
}
if(hitt0) *hitt0 = t0;
if(hitt1) *hitt1 = t1;
return true;
}
对于平板上的两个平面,这个例程要计算两个光线和它们的交点,得到交点处相应的参数t值。先考虑沿x轴的平板,它可以用分别过点(x1,0,0)和点 (x2,0,0)的两个平面来表达,它们的法向量都是(1,0,0)。考虑第一个交点,根据第3.4.3节的光线/平面求交公式,有:
t1 = -(( o – (x1,0,0)).(1, 0,0)) / (d . (1,0,0))
由于法向量的y,z分量都为零,我们有下面的简化形式:
t1 = – (ox – x1) / dx = (x1 – ox) / dx
实现代码首先要计算光线方向的相应分量的倒数,然后用它做乘法因子(因为乘法比除法快很多)。注意我们没有必要检查该分量是否为零。如果它为零,invRayDir将是正或负无穷大,算法仍然正常工作(这里假定系统使用IEEE 1985浮点计算标准)。
float invRayDir = 1.f / ray.d;
float tNear = (pMin – ray.o) * invRayDir;
float tFar = (pMax – ray.o) * invRayDir;
两个参数距离分别放在tNear和tFar中。所得到的这个参数区间[tNear, tFar]跟当前的参数区间[t0,t1]求交集,就得到新的当前参数区间。如果结果为空(即t0 > t1),则代码立即返回失败。有个跟浮点计算有关的小细节:如果光线原点在包围盒的平板上,并且光线和平板平面重合,那么tNear或tFar有可能被计算为0/0的形式,即是IEEE浮点数NaN(not a number)。跟无穷大值一样,在IEEE标准中NaN也有明确的语义:例如任何跟NaN相关的逻辑比较都返回假。因此,更改t0和t1的代码要小心地处理tNear和tFar为NaN的情况,使得t0或t1的值保持不变,而不至于变为NaN。
if(tNear > tFar) swap(tNear, tFar);
t0 = tNear > t0 ? tNear : t0;
t1 = tFar > t1 ? tFar : t1;
if(t0 > t1) return false;
4.3 网格加速器(Grid Accelerator)
GridAccel加速器把一个和轴对齐的空间区域划分成大小相同的块(称为体元,voxel)。 每一个体元存有那些和它重叠的体素的引用。给定一条光线,加速器按着光线穿过的每个体元的先后次序进行交点测试,而且只有和体元中记录的体素进行测试。无用的光线求交测试次数被大大地减少了,因为离光线比较远的体素根本就不予考虑。还有,因为体素是按沿光线从近到远的次序进行,一旦找到一个交点,就不必做近一步的求交测试了,因为不可能有更近的交点了。
GridAccel的初始化很快,决定沿光线的体元的考察次序也很容易确定。但是这种简单性是把双刃剑。如果场景中的体素并不是均匀分布的,GridAccel的性能会很差。如果一个很狭小的区域含有大量的几何体,这些几何体会都落在同一个体元中,性能就会很差,因为只要光线穿过这个体元,就会有大量的求交计算。这就是所谓的“体育场中的茶壶”问题。这里的基本问题是它的数据结构不能对其所存放的数据做很好地调整: 如果网格划分太细了,很多时间耗费到大量的空体元中;如果划分太粗了,就体现不出加速器的好处了。下一节的KdTreeAccel可以对几何体的分布有很好的自适应性,从而避免了这样的问题。
class GridAccel : public Aggregate {
public:
private:
};
4.3.1 创建
GridAccel构造器用一个vector来存储网格中的Primitive。它根据体素的个数来自动决定体元的个数。
其中一个增加网格实现的复杂性的因素是,有些体素是不可以直接求交的(调用Primitive::CanIntersect()会返回false), 必须把它们加以细化成子体素才可以求交。当创建网格时,这就可能成问题,因为场景中也许只有一个不可以直接求求交的体素,算法就决定只为场景划分成很粗的 几个体元。然而,如果我们再对这个体素进行细化时,它有可能化为上百万个体素,这个很粗的网格的加速求交测试的效率就太差了。pbrt是这样解决这个问题的:
· 如果网格的构造器中refineImmediately标志为真,则所有不可直接求交的体素都被细化为可求交的体素。这也许很浪费时间和内存,因为有些体素根本没必要进行细化,因为没有光线跟它们相交。
· 否则的话,只有当光线进入体素所重叠的一个体元时,才细化体素。如果细化出多个体素,新体素就被放入一个新的GridAccel实例中,并用之代替原被细化的体素。这样做的目的是每次细化一个体素就不必重建整个网格。有一个传给GridAccel构造器的标志forRefined,用来表示这个网格构造器是为pbrt显式调用,还是由于Refined()被调用的。这个标志跟信息统计有关。
GridAccel::GridAccel(const vector
bool forRefined, bool refinedImmediately)
: gridForRefined(forRefined) {
}
Bool gridForRefined;
首先,构造器确定存储在网格中的体素,根据refineImmediately标志,要么直接使用传进来的vector,要么对所有传入的体素加以细化。
vector
if(refineImmediately)
for(u_int i = 0; i
else
prims = p;
因为体素可以和多个网格上的体元相重叠,当光线穿过这些体元时,有可能跟同一个体素进行多次求交测试。我们用一个叫做“信箱检查”(mailboxing)的技术快速地检查一条光线是否跟一个特定的体素进行过测试,这样就避免了多余的测试。在这种技术中,每条光线都有一个整数编号。上一次的测试中的光线编号和被测试的体素一起被记录下来。当光线穿过这些体元跟其中每个体素进行测试时,就要比较光线的编号和体素的编号;如果两者不同,则进行求交测试,并把体素的编号改成光线的编号;如果相同,这说明光线碰到了同一个体素,就可以跳过这个测试了。
GridAccel构造器为每个体素创建一个MailboxPrim结构。网格体元存放指向那些跟它重叠的那些体素的MailboxPrim的指针。MailboxPrim存放一个对体素的引用和上次测试过的光线的编号。所有的信箱都在一个连续的单个内存区,以提高内存效率。
nMailBoxes = prims.size();
mailboxes = (MailboxPrim *)AllocAligned(nMailboxes *
sizeof(MailboxPrim));
for(u_int i = 0; i < nMailBoxes; i++)
new (&mailboxes) MailboxPrim(prim);
struct MailboxPrim {
MailboxPrim(const Reference
primitive = p;
lastMailboxId = -1;
}
Reference
int lastMailboxId;
};
u_int nMailboxes;
MailboxPrim *mailboxes;
构造器下一步要做的工作是计算包围所有体素的包围盒,并决定沿x,y,z轴划分多少个体元。变量voxelPerUnitDist给出沿三个轴方向划分的每单位长度上的体元数。有了这个值,乘以每个方向上的包围盒长度,即得到该方向上的体元数。每个方向的体元数被限制在64个,从而避免产生过于庞大的数据结构。
for(u_int i = 0; i < prims.size(); ++i)
bounds = Union(bounds, prims->WorldBound());
Vector delta = bounds.pMax – bounds.pMin;
for(int axis = 0; axis < 3; ++axis) {
NVoxels[axis] = Round2Int(delta[axis] * voxelPerUnitDist);
NVoxels[axis] = Clamp(NVoxels[axis], 1, 64);
}
int NVoxels[3];
BBox bounds;
作为估算体元的大小的第一步,我们应该使体元总数跟体素的总数成正比例。如果体素是均匀分布的,那么每个体元大致有相同数目的体素。如果我们增加体元个数,那么每个体元上的体素个数就会减少(也减少了需要光线和体素的求交测试),从而提高了效率。但这样做也会增加内存开销,降低缓存性能,并增加了光线遍历体元的时间。另一方面,太少的体元会导致低效率,因为光线和体素的求交测试次数增加了。
为了使得体元个数跟体素个数成正比例,我们可以取物体个数的立方根 再乘以某个因子。在pbrt中,这个因子是3。对于N个体素而言,我们令包围盒最长的一侧有3N1/3个体元,而另两侧的设置要保证体元是大致的立方体。变量voxelsPerUnit是这三个计算的基础,它给出了单位距离上的体元个数,这个值可以使得包围盒最长的一侧有3N1/3个体元。
int maxAxis = bounds.MaximumExtent();
float invMaxWidth = 1.f / delta[maxAxis];
float cubeRoot = 3.f * powf(float(prim.size()), 1.f/3.f);
float voxelsPerUnitDist = cubeRoot * invMaxWidth;
给定了每个轴方向上的体元个数,构造器把GridAccel::Width设置成体元在世界空间内的宽度,并计算出它的倒数GridAccel::InvWidth(为了提高效率)。最后,它为网格申请一个指向Voxel结构的指针数组,每个体元对应数组中的一个Voxel指针。这些指针初始化为NULL,只有一个或多个体素跟它重叠时,才会申请空间。
for (int axis = 0; axis < 3; ++axis) {
Width[axis] = delta[axis] / NVoxels[axis];
InvWidth[axis] = (Width[axis] == 0.f) ? 0.f : 1.f / Width[axis];
}
int nVoxels = NVoxels[0] * NVoxels[1] * NVoxels[2];
voxels = (Voxel **) AllocAligned(nVoxels * sizeof(Voxel *));
memset(voxels, 0, nVoxels * sizeof(Voxel *));
Vector Width, InvWidth;
Voxel **voxels;
一旦体元自己申请了Voxel空间,就可以把跟它重叠的体素加入进去。GridAccel构造器还把体素对应的MailboxPrim加入到跟其重叠的体元中。
for (u_int i = 0; i < prims.size(); ++i) {
}
首先,我们把体素的世界空间中的包围盒转换成整数的体元坐标(分别包含包围盒的两个对角)。GridAccel::PosToVoxel()把世界坐标(x,y,z) 变换成包含该点的体元坐标。
BBox pb = prim ->WorldBound();
int vmin[3], vmax[3];
for(int axis = 0; axis < 3; ++axis) {
vmin[axis] = PosToVoxel(pb.pMin, axis);
vmax[axis] = PosToVoxel(pb.pMax, axis);
}
int PosToVoxel(const Point &P, int axis) const {
int v = Float2Int((P[axis] – bounds.pMin[axis]) * InvWidth[axis]);
return Clamp(v, 0, NVoxels[axis] – 1);
}
GridAccel::VoxelToPos()函数跟GridAccel::PosVoxel()函数正好相反;它返回体元的下端的一角的坐标。该函数有两个形式,第一个只为一个轴计算,第二个为三个轴计算。
float VoxelToPos(int p, int axis) const {
return bounds.pMin[axis] + p * Width[axis];
}
Point VoxelToPos(int x, int y, int z) const {
return bounds.pMin + Vector(x * Width[0], y * Width[1], z * Width[2]);
}
现在我们可以把体素加入到跟它的包围盒重叠的体元中去了。用包围盒进行重叠测试是比较保守的方法,最坏的情况是多估算了重叠体元个数。下图表示了两种情况,用这种方法把体素放到了不必要的体元里。
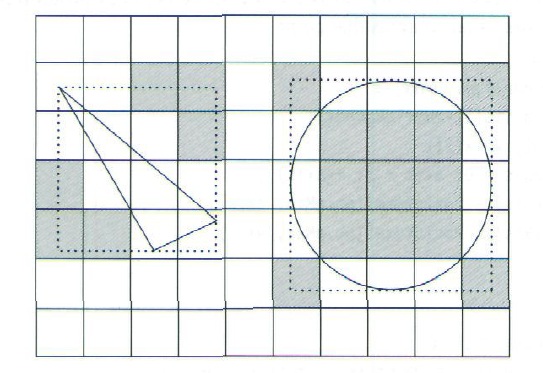
for (int z = vmin[2]; z < vmax[2]; ++z)
for (int y = vmin[1]; y < vmax[1]; ++y)
for (int x = vmin[0]; x < vmax[0]; ++x) {
int offset = Offset(x,y,z);
if(!voxel[offset]) {
}
else {
}
}
GridAccel::Offset()辅助函数给出体元(x,y,z)在体元数组的偏置值。这里使用的是C++把多维数组编码到一维数组中的标准索引方法。我们把它写成单独一个函数,是为了提高缓存性能,并且更方便地使用其它不同的数组数据排列方式,比如块方式(blocked scheme)。
inline int Offset(int x, int y, int z) const {
return z * NVoxels[0] * NVoxels[1] + y * NVoxels[0] + x;
}
为了进一步地减少体元所用的动态申请的内存,并改进它们的内存局部性,网格的构造器用一个ObjectArena为体元提供内存。ObjectArena类在第A.2.4节有所介绍,它提供了基于大块内存的内存分配例程。它并不为每次的内存分配释放内存,而是一次把所有内存释放掉。这就改进了内存分配性能,实际上也减少了维护内存使用的开销,也就减少了系统的内存使用。
voxels[offset] = new (voxelArena) Voxel(&mailboxes);
ObjectArena
如果这不是第一个覆盖该体元的体素,那么该体元已经被分配了一个Voxel,我们就直接调用Voxel::AddPrimitive()把该体素加入到体元中。
voxels[offset]->AddPrimitive(&mailboxes);
Voxel结构记录了有哪些体素跟它的区域重叠。由于一个网格有许多体元,我们用一些简单的技术来保证Voxel占很少的内存: 它的基本性质被打包在一个32位的字中,并用union来覆盖两个指针,具体使用哪个指针由体素的个数来定。这样做的好处是改善了缓存的性能,从而使得系统的性能也提高了。
struct Voxel {
union{
MailboxPrim *onePrimitive;
MailboxPrim **primitives;
};
u_int allCanIntersect:1;
u_int nPrimitives:31;
};
当一个Voxel刚被分配时,只找到一个体素跟它重叠,Voxel::nPrimitives为1,我们用Voxel::onePrimitive来存放指向它的MailboxPrim的指针。如果发现了更多的重叠的体素,Voxel::nPrimitives就大于1了,Voxel::primitives就用来存放指向MailboxPrim结构的动态申请的指针数组。由于这两种情况是互斥的,所以我们可以用union所代表的同一个内存地址,它即可以是指向单个体素的指针,也可以是指向多个体素的指针数组。Voxel::allCanIntersect用来记录是否体元中所有的体素都可以求交,或者其中有些体素需要细化。
Voxel(MailboxPrim *op) {
allCanIntersect = false;
nPrimitives = 1;
onePrimitive = op;
}
一旦Voxel::AddPrimitive()被调用,就意味着有两个或多个体素跟该体元重叠,体素的MailboxPrim指针就要被存放在体元的primitives数组中。关于该数组的内存分配有两种情况:如果体元只有一个体素而现在需要存放第二个体素;或者,数组已经满了。这里的代码没有用额外的内存空间记录数组的大小,而是约定数组大小必须是2的幂值。一旦Voxel::nPrimitives是2的某次幂值,数组就已经被填满了,需要申请更多的空间。
void AddPrimitive(MailboxPrim *prim) {
if(nPrimitives == 1) {
}
else if(IsPowerOf2(nPrimitives)) {
}
primitives[nPrimitives] = prim;
++nPrimitives;
}
回忆一下:Voxel::onePrimitive和Voxel::primitives是存放在同一个union中的。因此,有必要把指针数组的新内存地址放置在一个局部变量中,再把它的第一个成员初始化成Voxel::onePrimitive,然后才可以把Voxel::primitives设置成这个指针数组的地址。否则,Voxel::onePrimitive就被覆盖掉了,因为Voxel::onePrimitive和Voxel::primitives共享同一个内存位置。
MailboxPrim **p = new MailboxPrim *[2];
p[0] = onePrimitive;
primitives = p;
类似地,但我们扩充MailboxPrim的指针数组时,也要小心地设置Voxel::primitives。
int nAlloc = 2 * nPrimitives;
MailboxPrim **p = new MailboxPrim *[nAlloc];
for(u_int i = 0; i < nPrimitives; ++i)
p = primitives;
delete[] primitives;
primitives = p;
我们这里略去GridAccel::WorldBound()和GridAccel::CanIntersect()和GridAccel析构器,因为它们的实现是直截了当的。
4.3.2 遍历
GridAccel::Intersect()函数的任务是确定光线穿过哪些体元,并调用相应的光线-体素求交例程。
bool GridAccel::Intersect(const Ray &ray,
Intersection *isect) const {
}
第一个任务是决定光线是在哪里进入网格的,这就可以知道体元遍历的起始位置。如果光线原点在网格的包围盒之内,很显然,它的起始位置就是原点所在的体元。否则,GridAccel::Intersect()函数寻找光线跟网格包围盒的交点, 如果发现交点,则沿光线的第一个交点就是开始点。如果没有跟包围盒的交点,那么光线和网格中的任何体素都没有交点,整个函数就可以立即返回了。
float rayT;
if(bounds.Inside(ray(ray.mint)))
rayT = ray.mint;
else if(!bounds.IntersectP(ray, &rayT))
return false;
Point gridIntersect = ray(rayT);
下一个任务是确定一个用于信箱检查技术(mailboxing)中的光线编号。GridAccel用一个单调增加的序列作为光线的编号,这个序列是由静态变量GridAccel::curMailboxId生成的。
int rayId = ++curMailboxId;
static int curMailboxId;
求交函数现在可以计算该光线的起始位置的体元坐标(x,y,z) 和其它几个用来帮助体元遍历的辅助值。光线-体元遍历算法实质上跟Bresenham直线绘制算法相同的,Bresenham算法只用加法和比较运算来找出直线穿过的像素。这里的算法和Bresenham算法的主要区别是我们要找出所有跟光线相交的体元,而Bresenham算法只是在每一行或列中绘出一个像素。这类算法被称为数字微分分析法(DDA)。
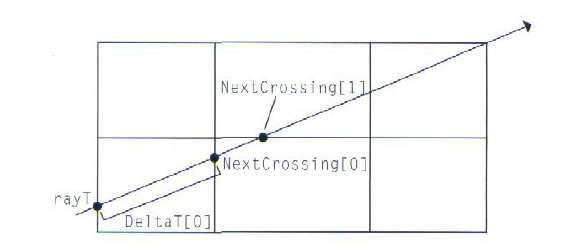
在整个光线-体元遍历算法中,我们要记录下列变量:
1. 当前正在被考虑的体元坐标Pos。
2. 光线在x,y,z三个方向上和下一个体元相交的三个参数t值NextCrossT。例如,对于一条有正值x方向分量的光线而言,NextCrossT[0]就是参数起始点rayT加上到下个体元的x距离除以光线的x方向分量(这跟光线-平面求交公式类似)。
3.走到下一步后,当前体元的坐标在每个方向上的变化(-1,1),存放在Step内。
4.光线在每个方向上沿光线方向走一个体元的参数距离,DeltaT。这些值可以由相应方向上的体元宽度除以光线在相应方向上的方向分量得到。
5.光线走出网格时的最后一个体元的坐标,Out。
前两项变量要在每一步体元遍历时修改,而后三项对每条光线而言是不变的。
float NetCrosssing[3], DeltaT[3];
int Step[3], Out[3], Pos[3];
for(int axis = 0; axis < 3; ++axis) {
if(ray.d[axis] >= 0) {
} else {
}
}
计算光线开始的体元地址是很容易的,因为这个函数已经知道光线进入网格的位置,只需调用工具函数GridAccel::PosToVoxel()即可。
Pos[axis] = PosToVoxel(gridIntersect, axis);
如果光线的某个轴上的方向分量为0,那么下面所列出的计算把NextCrossingT在该轴上的值初始化为IEEE浮点无穷大值,在本节后面所介绍的体元遍历保证不会沿这个方向走。
NextCrossing[axis] = rayT +
(VoxelToPos(Pos[axis]+1, axis) – gridIntersect[axis] / ray.d[axis];
Delta[axis] = Width[axis] / ray.d[axis];
Step[axis] = 1;
Out[axis] = NVoxels[axis];
类似地,可以求出当光线方向分量为负值的这些值。
NextCrossing[axis] = rayT +
(VoxelToPos(Pos[axis]+1, axis) – gridIntersect[axis] / ray.d[axis];
Delta[axis] = -Width[axis] / ray.d[axis];
Step[axis] = -1;
Out[axis] = -1;
一旦光线的所有准备工作完成后,就可以遍历光线所经过的体元了。从第一个体元开始,求交例程检查体元内的体素和光线的交点。如果有交点,则设置hitSomething为真。要注意因为体素可能和多个体元重叠,交点可能在当前体元之外。因此,当找到一个交点后,函数并不马上返回,而是利用了体素求交函数会修改光线的Ray::maxt的这个事实。因此,只有当光线进入一个体元的进入点比最近交点还要远才返回。
bool hitSomething = false;
for(;;){
Voxel *voxel = voxels[Offset(Pos[0], Pos[1], Pos[2])];
if(voxel != NULL)
hitSomething |= voxel->Intersect(ray, isect, rayId);
}
return hitSomething;
对于每个非空体元,函数调用Voxel的Intersect()例程,该例程处理“信箱检查”(mailboxing)的细节并调用Primitive::Intersect()。
bool Voxel::Intersect(const Ray &ray, Intersection *isect, int rayId) {
}
Voxel::allCanIntersect布尔成员变量用来指示是否所有的体素是可求交的。如果该值为 false,Intersect()例程必须对所有的体素进行循环,必要时调用它们的细化例程,直到所有的体素都是可求交的。要注意由于多一层指针间接引用(因为在体元中单个体素的存放和多个体素的存放是不同的),查找第i个MailboxPrim的逻辑有些复杂。见下面的代码对这个情况的处理:
if (!allCanIntersect) {
MailboxPrim **mpp;
if(nPrimitives == 1) mpp = &onePrimitive;
else mpp = primitive;
for(u_int i = 0; i < nPrimitives; ++i) {
MailboxPrim *mp = mpp;
}
allCanIntersect = true;
}
所有需要细化的体素都被细化,最后所有的体素都是可求交的。如果有多个体素返回,则创建一个新的GridAccel,用来存放被返回的多个体素。这样做的原因是为了简化体素细化,因为这样不会增加体元中体素的个数。如果该体素跟多个体元向重叠,由于它们都有指向同一个MailboxPrim的指针,所以只需直接修改这个被共享的MailBoxPrim中的体素引用,而没有必要对相关所有的体元循环并修改。
if(!mp->primitive->CanIntersect()) {
vector
mp->primitive->FullyRefine(p);
if(p.size() == 1)
mp->primitive = p[0];
else
mp->primitive = new GridAccel(p, true, false);
}
一旦确定体元中所有的体素都是可求交的,就可以对这些体素所对应的MailboxPrim进行逐个地进行求交测试。同样地,这个循环也要注意对只含一个体素和含有多个体素的体元的处理的差别。
bool hitSomething = false;
MailboxPrim *mpp;
if(nPrimitives == 1) mpp = &onePrimitive;
else mpp = primitives;
for(u_int i = 0; i < nPrimitives; ++i) {
MailboxPrim *mp = mpp;
}
return hitSomething;
现在要做信箱检查了。如果该光线跟该体素在另一个体元进行过求交测试了,就可以跳过这个多余的求交测试了。
if(mp->lastMailboxId == rayId)
continue;
最后,如果有必要进行光线-体素求交测试,就要更新体素的信箱。
mp->lastMailboxId = rayId;
if(mp->primitive->Intersect(ray, isect)) {
hitSomething = true;
}
做完当前体元中的体素求交测试后,就要沿着光线进入下一个体元。网格必须确定下一步是在x方向,y方向,还是z方向。幸运地是,NextCrossingT给出了每个方向上光线的下一个交叉点的参数距离,只需选择最小值所在的轴即可。如果下一步走出了网格,或者所选择的NextCrossingT的值被已找到的交点还要远,遍历就结束了。否则,就要进入下一个选定的体元,并更新选定方向上的NextCrossingT(加上DeltaT),这样将来的遍历会知道要走多远才可以回到这个方向上。
if(ray.maxt < NextCrossingT[stepAxis])
break;
Pos[stepAxis] += Step[stepAxis];
if(Pos[stepAxis] == Out[stepAxis])
break;
NextCrossingT[stepAxis] += DeltaT[stepAxis];
选定下一步的方向需要求三个值的最小值,这是很简单的。然而,我们可以做些优化,使得不用条件语句就可以求得所要找的方向(减少分支语句对CPU的性能影响)。(这个技巧可以从下列代码中看出来,这里不多说了)。
int bits = ((NextCrossingT[0] < NextCrossingT[1]) << 2) +
((NextCrossingT[0] < NextCrossingT[2]) << 1) +
((NextCrossingT[1] < NextCrossingT[2]));
const int cmpToAxis[8] = { 2, 1, 2, 1, 2, 2, 0, 0 };
int stepAxis = cmpToAxis[bits];
网格加速结构还提供了一个特殊的GridAccel::IntersectP()函数,用来检查沿阴影光线上的求交检查,我们只需要知道是否有交点,而不需要知道交点的细节。它跟GridAccel::Intersect()几乎相同,只不过它要调用Primitive::IntersectP()而不是Primitive::Intersect(),而且只有发现交点存在就立即返回。它的实现就不列在这里了。
bool IntersectP(const Ray &ray) const;
Categories: Garfield's Diary
